Με την αλλαγή του χρόνου, βρίσκω αφορμή να γράψω για κάτι που έχω στο μυαλό μου εδώ και πολύ καιρό και αυτό είναι το θέμα του χρόνου στη Σχετικότητα ειδικά και στη φυσική γενικότερα. Το θέμα αυτό με απασχολεί εδώ και πολύ καιρό.
Την εκπομπή της ΕΤ3, «Το Σύμπαν που Αγάπησα», την γνωρίζει ο περισσότερος κόσμος. Είναι ίσως η πιο γνωστή επιστημονική σειρά ντοκιμαντέρ της Ελληνικής τηλεόρασης, με πολλούς "φανατικούς" οπαδούς, που έχει δεχθεί και βραβεία. Ιδιαιτερότητα της εκπομπής είναι ότι οι ίδιοι οι παρουσιαστές είναι μέλη της πανεπιστημιακής κοινότητας και συγκεκριμένα είναι ο αναπληρωτής καθηγητής Στράτος Θεοδοσίου και ο επίκουρος καθηγητής Μάνος Δανέζης.
Η βασική θεματολογία της εκπομπής είναι γύρω από θέματα σχετικά με την Αστροφυσική γενικά και ειδικότερα την Κοσμολογία, αλλά και τις σύγχρονες φυσικές θεωρίες όπως είναι για παράδειγμα η θεωρία της Σχετικότητας. Η εκπομπή ακόμα πραγματεύεται και ζητήματα Φιλοσοφίας και Ιστορίας της Επιστήμης. Τα τελευταία δεν θα με απασχολήσουν στο συγκεκριμένο post, αν και έχω και εκεί τους προβληματισμούς μου.
Το θέμα που θα με απασχολήσει, έχει να κάνει και με την ορθότητα της παρουσίασης μίας αρκετά βασικής επιστημονικής έννοιας τόσο συνολικά όπως την συναντάμε στη φυσική όσο και ειδικότερα όπως την συναντάμε στην Κοσμολογία. Δηλαδή θα ασχοληθώ και με την ορθότητα της παρουσίασης στα πλαίσια της εκπομπής «Το Σύμπαν που Αγάπησα», της έννοιας του χρόνου στην φυσική γενικά και στην Κοσμολογία ειδικότερα.
Ίσως θα πρέπει να επισημάνω ότι το πρόβλημα με την συγκεκριμένη εκπομπή, δεν είναι μόνο η λάθος παρουσίαση των σχετικών με τον χρόνο και την Κοσμολογία, αλλά και ένα πλήθος άλλων παρόμοιων σφαλμάτων και παρανοήσεων που οδηγούν σε διάφορα "μονοπάτια" ενώ παρουσιάζονται ως δεδομένη επιστημονική γνώση, με την "βούλα" κιόλας δύο καθηγητών Αστροφυσικής του πανεπιστημίου της Αθήνας. Φυσικά αυτό το θέμα είναι ακόμα πιο πλατύ και δύσκολο και περιλαμβάνει ένα ευρύτερο φάσμα περιπτώσεων "επιστημονικής παραπληροφόρησης" από "ειδικούς" και μη και δεν θα ασχοληθώ περισσότερο εδώ.
Ξεκινάμε λοιπόν με το θέμα του χρόνου στην Κοσμολογία. Παρακάτω παραθέτω δύο σχετικά βίντεο. Το πρώτο είναι απόσπασμα από την ίδια την εκπομπή και συγκεκριμένα ένα επεισόδιο του 3ου κύκλου, ενώ το δεύτερο είναι από μία συνέντευξη, όπου παρουσιάζεται η αντίληψη των δύο καθηγητών για τον χρόνο και την μέτρησή του, στα πλαίσια της κοσμολογίας του Big Bang. Όπως φαίνεται στο δεύτερο βίντεο, με τις απόψεις αυτές που παρουσιάζονται, μάλλον συμφωνεί και ο κ. Αγγελόπουλος, τότε πρόεδρος της Ένωσης Ελλήνων Φυσικών και αναπληρωτής καθηγητής του τομέα Πυρηνικής Φυσικής του πανεπιστημίου Αθηνών.
Η ηλικία του Σύμπαντος -- Ο Χρόνος στην κοσμολογία
Δανέζης για τον χρόνο στην Κοσμολογία
Για όποιον βαρέθηκε να δει τα βίντεο, η άποψη για τον χρόνο συνοψίζεται στην περιγραφή του 1ου βίντεο από το YouTube, που παραθέτω παραπάνω.
Ωραία. Για να απαντηθεί το θέμα που τίθεται, θα πρέπει να τα πάρουμε τα πράγματα λίγο από την αρχή. Να ξεκινήσουμε δηλαδή να συζητάμε για το τι είναι ο χρόνος και ποια η σημασία του, στα πλαίσια της ειδικής σχετικότητας αρχικά και της γενικής σχετικότητας στη συνέχεια. Το μόνο που θα χρειαστεί ως δεδομένο στην όλη συζήτηση, είναι μια βασική αίσθηση γεωμετρίας.
Τι είναι λοιπόν ο χωροχρόνος; Για έναν φυσικό (δηλαδή με άλλα λόγια, για κάποιον που θέλει να κάνει φυσική, δηλαδή να μετρήσει, να παρατηρήσει και να υπολογίσει πράγματα), ο χωροχρόνος είναι ένα σύνολο από «γεγονότα». Όπως το λέει πολύ όμορφα ο R. Geroch (“General Relativity from A to B”, Chicago Press), ένα γεγονός είναι το σκάσιμο μίας κροτίδας ή ένα χτύπημα των δαχτύλων. Ένα «γεγονός» λοιπόν είναι κάτι περιορισμένο στον χώρο και τον χρόνο, το ισοδύναμο ενός μαθηματικού σημείου. Έτσι λοιπόν ο χωροχρόνος αποτελείται από γεγονότα. Ένα πιο «φυσικό» παράδειγμα γεγονότος, είναι η σκέδαση ενός ηλεκτρονίου από ένα φωτόνιο. Η στιγμή της σκέδασης είναι ένα γεγονός. Αντιθέτως, το ίδιο το ηλεκτρόνιο, δεν είναι «γεγονός», αφού αποτελεί κάτι που έχει έκταση, αν όχι στον χώρο τουλάχιστον στον χρόνο. Και εδώ ερχόμαστε στο δεύτερο βασικό συστατικό του χωροχρόνου, τις «κοσμικές γραμμές». Κάθε σωματίδιο, αποτελεί και μία κοσμική γραμμή που εκτείνεται στον χρόνο. Για μία τέτοια κοσμική γραμμή, αν προσδιορίσουμε ένα γεγονός επάνω της, τότε μπορούμε να μιλήσουμε για το «μέλλον» και το «παρελθόν» αυτού του γεγονότος, κατά μήκος της κοσμικής γραμμής. Σε αυτή τη φάση τις έννοιες «μέλλον» και «παρελθόν», τις αναφέρω κάπως αυθαίρετα, αφού δεν έχουμε μιλήσει για το τι σημαίνει ο χρόνος, πράγμα που θα κάνω παρακάτω.
Έτσι λοιπόν, τα βασικά συστατικά του χωροχρόνου είναι τα γεγονότα και οι κοσμικές γραμμές. Με αυτά τα συστατικά και μόνο μπορούμε να μιλήσουμε για χωροχρόνο, χωρίς να χρειάζεται να βάλουμε στη συζήτηση πράγματα όπως «συστήματα συντεταγμένων» και διάφορα άλλα τέτοια. Φυσικά, εμείς δεν είμαστε ικανοποιημένοι μόνο με αυτό. Το ζητούμενο, προκειμένου να κάνει κανείς φυσική, είναι να μιλήσει για την σχέση ανάμεσα σε γεγονότα, δηλαδή να μπορεί να απαντήσει σε ερωτήσεις του τύπου, «το γεγονός Α συμπίπτει με το γεγονός Β;», «το γεγονός Α συνέβη πριν το γεγονός Β;» και διάφορες άλλες τέτοιες ερωτήσεις.
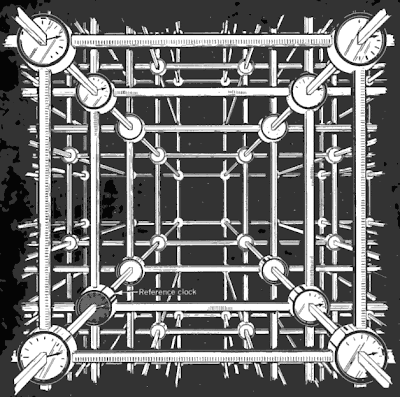
Άρα, εδώ τίθεται το ζήτημα της μέτρησης. Πώς μετράμε στη σχετικότητα ότι έχει σχέση με τα γεγονότα που μας ενδιαφέρουν; Η απάντηση είναι, «μετράμε με τον απλούστερο δυνατό τρόπο, δηλαδή με ράβδους και ρολόγια». Η υλοποίηση αυτής της μετρητικής διαδικασίας είναι ο «παρατηρητής». Ο παρατηρητής, δηλαδή είναι εν γένει μια ιδανική μετρητική συσκευή, εφοδιασμένη με ρολόγια και ράβδους, με τα οποία μετρά χρόνο και αποστάσεις. Μια καλή οπτικοποίηση ενός παρατηρητή είναι αυτή που δίνουν οι Taylor και Wheeler ("Spacetime Physics", W.H.Freeman) όπου ο παρατηρητής είναι ένα πλέγμα από ράβδους και ρολόγια, όπου κάθε ράβδος έχει κάποιο συγκεκριμένο μήκος και σε κάθε κόμβο του πλέγματος υπάρχει ένα ρολόι. Έτσι σε κάθε γεγονός αποδίδουμε κάποιο χρόνο και κάποια θέση σύμφωνα με την παρακάτω διαδικασία: για κάποιο γεγονός που συμβαίνει, του αποδίδουμε τον χρόνο που καταγράφει το κοντινότερο ρολόι στο γεγονός, ενώ για την θέση, του αποδίδουμε την θέση του ίδιου ρολογιού. Ακόμα δεν έχουμε καθορίσει τι είναι αυτός ο χρόνος ή η θέση, αλλά θα το κάνουμε σύντομα. Φυσικά, ανάλογα με την ακρίβεια που θέλουμε, μπορούμε να κάνουμε τα μήκη των ράβδων οσοδήποτε μικρά, καθώς και την ακρίβεια των ρολογιών μας, έτσι ώστε να καλύπτουμε όσο πυκνά θέλουμε όλον τον χώρο και τον χρόνο. Από την παραπάνω εικόνα φαίνεται ότι σε κάθε παρατηρητή, αντιστοιχεί και ένα σύστημα αναφοράς. Η ειδική κλάση των παρατηρητών και των συστημάτων που κινούνται ελεύθερα, χωρίς να επιταχύνονται ή να ασκούνται δυνάμεις επάνω τους, ονομάζονται αδρανειακοί παρατηρητές και αδρανειακά συστήματα αντίστοιχα. Αυτά τα συστήματα όπως τα περιγράψαμε ως πλέγμα, αποτελούν ουσιαστικά και ένα τύπο συστήματος συντεταγμένων, όπου για παράδειγμα ένα γεγονός αποκτά τις συντεταγμένες θέσης, ως προς ένα σημείο αναφοράς, του πλησιέστερου ρολογιού, δηλαδή 3 ράβδους κατά μήκος του ενός άξονα, 5 ράβδους κατά μήκος του άλλου άξονα και 1 ράβδο κατά μήκους του 3ου άξονα (θέση x,y,z) ενώ έχει και την καταγραφή ενός χρόνου από το αντίστοιχο ρολόι (χρόνος t). Πριν όμως προχωρήσουμε περισσότερο στις συντεταγμένες, πρέπει να επιστρέψουμε στο τι είναι ο χρόνος που μετράνε τα ρολόγια και η απόσταση που μετράνε οι ράβδοι.
Ο χρόνος και ο χώρος, είπαμε παραπάνω, ότι μετριέται με ρολόγια και ράβδους. Υπάρχει όμως το ερώτημα, μήπως κρύβεται κάτι περισσότερο πίσω από αυτό; Η απάντηση είναι όχι. Όλη η ουσία νομίζω ότι μπορεί να αποδοθεί με την παρακάτω διατύπωση από το πολύ καλό εκλαϊκευτικό βιβλίο του Hermann Bondi, «Σχετικότητα και κοινή λογική», που έχει μεταφραστεί από τις εκδόσεις Τροχαλία, η οποία είναι:
Η διατύπωση αυτή, κάνει απόλυτα σαφές τι σημαίνει χρόνος και χώρος. Χρόνος είναι αυτό που μετρά το ρολόι μου και χώρος είναι αυτό που μετρά η ράβδος μου. Το ίδιο ακριβώς πράγμα ξεκαθαρίζει και ο Einstein στην πρώτη εκείνη εργασία του 1905, «Επί της Ηλεκτροδυναμικής των Κινούμενων Σωμάτων». Συγκεκριμένα, παραθέτω από την μετάφραση του Θάνου Χριστακόπουλου, από τις εκδόσεις Τροχαλία, «Η ειδική θεωρία της Σχετικότητας (Τα πρωτότυπα άρθρα)»,
Η αναφορά αυτή του Einstein, εμφανίζει και τα ηλεκτρομαγνητικά φαινόμενα ως πρωταρχικής σημασίας για την θεωρία της σχετικότητας και αυτό οφείλεται στον σημαντικό ρόλο που παίζει η ταχύτητα του φωτός, ως μία σταθερά της ηλεκτρομαγνητικής θεωρίας (σε αυτό θα αναφερθούμε παρακάτω).
Η έμφαση που δίνεται σε αυτό το σημείο στο γεγονός ότι ο χρόνος για έναν παρατηρητή είναι αυτό που μετρά το ρολόι του (όπου φυσικά αυτό μπορεί να το δει κανείς σε οποιοδήποτε βιβλίο σχετικότητας και αν ανοίξει), έρχεται σε σαφή αντίθεση με αυτά που διατυπώνονται στα παραπάνω βίντεο ειδικά και στο σύνολο των συγκεκριμένων εκπομπών γενικά. Παρακάτω θα γίνει ακόμα πιο ξεκάθαρη η σημασία της διατύπωσης ότι «ο χρόνος ενός παρατηρητή είναι αυτός που μετράει το ρολόι του» και της καθολικότητας αυτής της πρότασης.
Ωραία, είπαμε μέχρι τώρα ότι τα θεμελιώδη συστατικά του χωροχρόνου είναι τα γεγονότα και οι κοσμικές γραμμές, όπου παράδειγμα των τελευταίων είναι τα στοιχειώδη σωματίδια όπως τα ηλεκτρόνια και τα φωτόνια, ενώ ορίσαμε και τι συνιστά μέσα στο χωροχρόνο ένας παρατηρητής, πως αυτός καθορίζει ένα σύστημα αναφοράς και ότι οι μετρήσεις σε αυτό το σύστημα γίνονται με ράβδους σταθερού μήκους και ρολόγια που εκτίνονται παντού γύρω του.
Το επόμενο ερώτημα είναι, πως ακριβώς μετράνε τα ρολόγια το χρόνο και πως ακριβώς μετράνε οι ράβδοι τα μήκη. Υπάρχει κάποιο ρολόι που να είναι καλύτερο από το άλλο; Και ποια είναι η σχέση του χρόνου που μετρά ένα ρολόι εδώ με το χρόνο που μετρά ένα ρολόι κάπου αλλού; Με άλλα λόγια, ποιος είναι ο καλύτερος φυσικός μηχανισμός για να μετρήσουμε τον χρόνο, αν υπάρχει αυτός, ή ποιος είναι ο καλύτερος φυσικός μηχανισμός για να μετρήσουμε αποστάσεις, αν υπάρχει αυτός, και τέλος, πως ακριβώς συγχρονίζουμε τα διάφορα ρολόγια μεταξύ τους. Ειδικά το τελευταίο αποτελεί και ιδιαιτέρως σημαντικό θέμα, αφού ακόμα και η απόδοση κάποιας χρονικής στιγμής σε ένα γεγονός είναι ζήτημα της σύγκρισης της στιγμής που έγινε το γεγονός με τον χρόνο που έδειξε κάποιο ρολόι, δηλαδή είναι ζήτημα συγχρονισμού.
Σε αυτό το σημείο, πρέπει να επισημάνουμε ότι η καθημερινή μας εμπειρία της μέτρησης του χρόνου με ρολόγια που μετράνε δευτερόλεπτα και της μέτρησης των αποστάσεων με χάρακες που μετράνε μέτρα, συσκοτίζει την ενότητα που υπάρχει ανάμεσα στον χώρο και τον χρόνο. Δηλαδή δημιουργεί μια φαινόμενη ποιοτική διαφοροποίηση ανάμεσα στα δύο. Το πρόβλημα αυτό έρχεται να το ξεπεράσει η μία από τις δύο αρχές της ειδικής σχετικότητας, η αρχή της σταθερότητας της ταχύτητας του φωτός. Και ο τρόπος που το κάνει αυτό έχει αρκετό ενδιαφέρον.
Εδώ αξίζει να αναφέρουμε την παραβολή με τις δύο σχολές τοπογράφων που παρουσιάζουν οι Taylor και Wheeler (“Spacetime Physics”, W.H.Freeman), η οποία μπορεί να μας διδάξει πολλά σημαντικά πράγματα για τις βάσεις της ειδικής σχετικότητας. Θα παραθέσω την παραβολή σε μετάφραση (σχετικά ελεύθερη):
Αυτή η παραβολή μας λέει πολλά ενδιαφέροντα πράγματα. Το πρώτο και σημαντικότερο ίσως, μας το λέει η αναφορά της «ιερής» διεύθυνσης Βορά-Νότου, η οποία μετριέται με άλλες μονάδες μέτρησης, δηλαδή μίλια, που σχετίζονται με μία σταθερά αναλογίας k με τις μονάδες μέτρησης στην διεύθυνση Ανατολής-Δύσης. Αυτό είναι σαφής αναφορά στον χρόνο και την μέτρησή του σε δευτερόλεπτα, ενώ η σταθερά αναλογίας αναφέρεται στην ταχύτητα του φωτός. Με δεδομένη την αρχή της σταθερότητας της ταχύτητας του φωτός, μπορούμε να θεωρήσουμε αυτή την ταχύτητα ως σταθερά αναλογίας ανάμεσα στον χρόνο και τον χώρο, αφού ο λόγος $$\reverse\opaque s / t$$ υποδεικνύει κάποια ταχύτητα, ενώ ο λόγος $$\reverse\opaque s / c$$ υποδεικνύει κάποιο χρόνο και από την άλλη το γινόμενο $$\reverse\opaque c t$$ υποδεικνύει κάποια απόσταση. Θεωρώντας λοιπόν την ταχύτητα του φωτός ως παγκόσμια σταθερά, μπορούμε να μετρήσουμε την απόσταση σε δευτερόλεπτα ή τον χρόνο σε μέτρα, με τον ίδιο τρόπο περίπου που στην επιφάνεια της Γης, σε κάποιο συγκεκριμένο τόπο όπου η επιτάχυνση της βαρύτητας είναι σταθερή, μετράμε το βάρος μας (που είναι δύναμη) σε κιλά. Πρακτικά πως μπορούμε να το κάνουμε όμως αυτό; Δηλαδή, πως θα φτιάξω εγώ πρακτικά τα ρολόγια ή τις ράβδους που αναφέραμε παραπάνω, που αποτελούν τον παρατηρητή και το σύστημα του;
Αν βάλω ως βάση μου τις στέρεες ράβδους, τότε μπορώ να μετράω τον χρόνο μου σε μέτρα με το παρακάτω ρολόι. Βάζω δύο καθρέφτες στα άκρα μίας ράβδου, μήκους μισού μέτρου και στέλνω έναν παλμό από τον ένα καθρέφτη, προς τον άλλον. Ο παλμός θα φτάσει στον άλλον καθρέφτη, όπου θα ανακλαστεί και θα επιστρέψει στον πρώτο καθρέφτη. Κάθε φορά που αυτός ο κύκλος θα επαναλαμβάνετε, το φως θα έχει διανύσει ακόμα ένα μέτρο, άρα θα έχει περάσει χρόνος ίσος με ένα μέτρο φωτός ή $$\reverse\opaque t=\frac{1m}{c}=\frac{1}{3}\times 10^{-8}s$$. Σε κάθε «τικ», το ρολόι μας θα μετρά τόσο χρόνο.
Αντίστοιχα, μπορώ να βάλω ως βάση τον χρόνο που καταγράφει κάποιο ρολόι. Έτσι, μετρώντας τον χρόνο που κάνει ένας παλμός φωτός για να πάει μέχρι κάποιο σημείο, να ανακλαστεί και να επιστρέψει (υποτυπώδες συσκευή ραντάρ), μπορώ να υπολογίσω την απόσταση σε δευτερόλεπτα ή αλλιώς για δύο δευτερόλεπτα που θα κάνει το φως να πάει και να έρθει, η απόσταση θα είναι $$\reverse\opaque x = c \times 1s =3\times 10^{8}m$$. Φυσικά, αυτή η απόσταση είναι τεράστια. Αυτός είναι και ο τρόπος που μετράμε αποστάσεις στην Αστρονομία, όπου οι συμβατικές μονάδες είναι πολύ μικρές. Έτσι, εκεί έχουμε το έτος φωτός. Φυσικά μπορούμε να μικρύνουμε όσο χρειάζεται την μονάδα μέτρησης του χρόνου, ώστε να μπορούμε να μετρήσουμε και μικρότερες αποστάσεις.
Από τα παραπάνω, φαίνεται ότι το αξίωμα της σταθερότητας της ταχύτητας του φωτός μας δίνεις την δυνατότητα να αντιμετωπίσουμε με τον ίδιο τρόπο και τον χώρο και τον χρόνο.
Κάποιος όμως και πάλι θα μπορούσε να επιμείνει στο ερώτημα του πως είμαστε σίγουροι ότι όλα τα ρολόγια, θα κρατάνε τον ίδιο ρυθμό όπου και να τα βάλουμε ή πως είμαστε σίγουροι ότι όλες οι ράβδοι θα έχουν το ίδιο μήκος όπου και να τις βάλουμε; Αρχικά, πρέπει να πούμε ότι μιλάμε για «ιδανικά ρολόγια» και «ιδανικές ράβδους» (ιδανικά στερεά σώματα δηλαδή). Ακριβώς ιδανικό ρολόι και ράβδος δεν υπάρχει στην φύση, αλλά μπορούμε να το προσεγγίσουμε σχεδόν όσο καλά θέλουμε. Για παράδειγμα, αρχικά τον χρόνο σε μεγάλη κλίμακα τον μετράγαμε με την αλλαγή των εποχών και σε μικρότερη κλίμακα με την αλλαγή της θέσης του Ήλιου. Αυτό ήταν ένα καλό ρολόι για τις τότε απαιτήσεις. Αργότερα, μετράγαμε το χρόνο με κλεψύδρες και κεριά για μεγαλύτερη ακρίβεια. Από την εποχή του Γαλιλαίου, μετράμε τον χρόνο με εκκρεμή, που έχουν την ικανότητα να κρατάνε με σχετικά καλή ακρίβεια την περίοδό τους σταθερή. Σήμερα, πετυχαίνουμε, σε εμπορικές χρήσεις, πολύ καλή ακρίβεια στη μέτρηση του χρόνου, μετρώντας τις ταλαντώσεις ενός κρύσταλλου χαλαζία, ενώ για ακόμα μεγαλύτερη ακρίβεια χρησιμοποιούνται τα ατομικά ρολόγια των οποίων η λειτουργία στηρίζεται στην μέτρηση της συχνότητας της μικροκυματικής ακτινοβολίας που εκπέμπουν ή απορροφούν κάποια άτομα Κεσίου κατά την αποδιέγερση ή την διέγερσή τους. Έτσι ουσιαστικά, επιλέγοντας το κατάλληλο φυσικό σύστημα, μπορούμε να αυξήσουμε μέχρι το επιθυμητό επίπεδο την ακρίβεια της μέτρησης του χρόνου, μετρώντας τις «ταλαντώσεις» του αντίστοιχου συστήματος. Εδώ βλέπουμε ουσιαστικά ότι και πάλι το φως και συγκεκριμένα η συχνότητά του αποτελεί ένα μέτρο για την μέτρηση του χρόνου (δεδομένης της σταθερότητας της ταχύτητάς του στο κενό). Κάτι ανάλογο ισχύει και για τα μήκη των ράβδων που μπορούμε να χρησιμοποιήσουμε, όπου και αυτά εξαρτώνται από τις ταλαντώσεις των ατόμων που αποτελούν κάποιο στερεό σώμα και είναι διατεταγμένα σε κάποιο πλέγμα. Έτσι, μία από τις πρώτες συμβάσεις για την μέτρηση του μήκους ήταν η χρήση πρότυπων ράβδων κατασκευασμένων από υλικό που είχε την ικανότητα να μην αλλάζει πολύ το μήκος του με την αλλαγή της θερμοκρασίας. Αργότερα και αυτό το πρότυπο αντικαταστάθηκε από ένα πρότυπο βασισμένο στο μήκος κύματος της ακτινοβολίας μίας φασματικής γραμμής που εκπέμπει το άτομο του Κρυπτού. Δηλαδή και πάλι μετράμε τα μήκη με την βοήθεια του φωτός μέσω κάποιας ενεργειακής μετάβασης ενός ατόμου. Έτσι το μόνο που μας μένει για να έχουμε πανομοιότυπες «ράβδους» και «ρολόγια» είναι να χρησιμοποιήσουμε τα αντίστοιχα άτομα ως πρότυπα. Ναι, αλλά αυτά τα άτομα θα μας δίνουν το ίδιο αποτέλεσμα στην μέτρηση του χώρου και του χρόνου όπου και να τα τοποθετήσουμε; Η απάντηση είναι, ναι. Αυτό μας το εξασφαλίζει η δεύτερη βασική αρχή της θεωρίας της σχετικότητας, η αρχή της αναλλοιώτητας των φυσικών νόμων, δηλαδή η αρχή που λέει ότι οι φυσικοί νόμοι πρέπει να είναι η ίδιοι παντού και να δίνουν το ίδιο αποτέλεσμα για ένα πείραμα, οπουδήποτε ή οποτεδήποτε και αν αυτό πραγματοποιηθεί.
Έτσι, οι δύο βασικές αρχές της θεωρίας της σχετικότητας, μας επιτρέπουν να μετράμε τα μήκη και τους χρόνους παντού μέσα στο σύστημά μας, δηλαδή με λίγα λόγια μας επιτρέπουν την κατασκευή αυτού του πράγματος που είπαμε ιδανικό παρατηρητή.
Και τώρα ερχόμαστε στο άλλο μεγάλο θέμα που αφορά το πώς μετράμε οπουδήποτε μέσα στο σύστημά μας. Έστω ότι έχουμε απλώσει τα ρολόγια μας και τις ράβδους μας σε όλο το χώρο. Θα πρέπει να ρυθμίσω τα ρολόγια που έχω τοποθετήσει, έτσι ώστε να δείχνουν τον «σωστό» χρόνο, δηλαδή θα πρέπει να συγχρονίσω όλα τα ρολόγια μεταξύ τους. Και πάλι, ο συγχρονισμός των ρολογιών γίνεται με την βοήθεια του φωτός. Έστω ότι έχουμε το δικό μας ρολόι και ένα ρολόι σε κάποια απόσταση από εμάς που βρισκόμαστε στο κέντρο του συστήματος (στο κέντρο των αξόνων x,y,z). Στέλνουμε έναν παλμό φωτός προς το άλλο ρολόι την στιγμή $$\reverse\opaque t_1=t_0-\Delta t$$. Αν ο παλμός αυτός ανακλαστεί και φτάσει πίσω σε εμάς την στιγμή $$\reverse\opaque t_2=t_0+\Delta t$$, τότε λέμε ότι την στιγμή που ανακλάστηκε ο παλμός στο άλλο ρολόι, αυτό θα πρέπει να δείχνει χρόνο $$\reverse\opaque t_0$$ προκειμένου τα δύο ρολόγια να είναι συγχρονισμένα. Έτσι, εφαρμόζοντας μία τέτοια διαδικασία σε κάθε απομακρυσμένο ρολόι, μπορούμε να συγχρονίσουμε όλα τα ρολόγια στο σύστημα αναφοράς μας. Η διαδικασία του συγχρονισμού βασίζεται και αυτή στο γεγονός ότι η ταχύτητα του φωτός είναι σταθερή και άρα ο χρόνος που χρειάζεται το φως για να πάει και να έρθει προς και από το άλλο ρολόι που είναι ακίνητο σε κάποια απόσταση από εμάς είναι σταθερός. Έτσι η στιγμή της ανάκλασης είναι στη μέση αυτού του χρονικού διαστήματος. Εδώ μπορεί κάποιος να αναρωτηθεί, γιατί επιλέγουμε αυτή τη διαδικασία συγχρονισμού και δεν στέλνουμε για παράδειγμα κάποιο τρίτο ρολόι από εδώ εκεί ώστε να συγχρονιστούν τα δύο απομακρυσμένα ρολόγια; Η απάντηση είναι ένα από τα πιο ενδιαφέροντα αποτελέσματα της θεωρίας της σχετικότητας. Ο χρόνος που μετρά ένα ρολόι εξαρτάται από την διαδρομή που ακολουθεί [1,2].
Αυτό μας φέρνει πίσω στην παραβολή με τους τοπογράφους και στην «Αρχή του Αναλλοίωτου της Απόστασης». Μέχρι τώρα έχουμε χρησιμοποιήσει την αρχή της σταθερότητας της ταχύτητας του φωτός για να φέρουμε στην ίδια βάση τον χώρο και τον χρόνο και για να συγχρονίσουμε τα ρολόγια ενός αδρανειακού παρατηρητή, ενώ έχουμε χρησιμοποιήσει την αναλλοιώτητα των φυσικών νόμων για να εξασφαλίσουμε ότι μπορούμε πάντα και παντού να κάνουμε τις μετρήσεις του χρόνου και του μήκους που χρειαζόμαστε. Η ιδέα του αναλλοίωτου της χωχροχρονικής απόστασης μας δίνει τώρα τη δυνατότητα να συγκρίνουμε τις μετρήσεις που πραγματοποιούν διαφορετικοί παρατηρητές σε διαφορετικά αδρανειακά συστήματα, αλλά ακόμα μας δίνει και την δυνατότητα να ορίσουμε τον χρόνο με απόλυτο τρόπο.
Η «Αρχή του Αναλλοίωτου της Απόστασης», όπως την περιγράψαμε στην παραβολή των τοπογράφων, ισχύει και για τα χωροχρονικά μήκη στην ειδική σχετικότητα, όπου αυτή τη φορά έχουμε το χωροχρονικό μέτρο $$\reverse\opaque ds^2=-c^2dt^2+dx^2+dy^2+dz^2$$ να είναι αναλλοίωτο. Αν έχουμε μια κοσμική γραμμή στον χωροχρόνο, μπορούμε τότε να μετρήσουμε το αναλλοίωτο χωροχρονικό μήκος της χρησιμοποιώντας την προηγούμενη σχέση. Το αποτέλεσμα αυτού του υπολογισμού θα είναι μια γεωμετρική ποσότητα την οποία οποιοσδήποτε παρατηρητής και να την μετρήσει θα την βρει να είναι η ίδια. Χρησιμοποιώντας αυτή την αναλλοιώτητα ανάμεσα στην μέτρηση τέτοιων μεγεθών από διαφορετικούς παρατηρητές, μπορεί να οδηγηθεί κανείς στους μετασχηματισμούς του Lorentz που συνδέουν τις μετρήσεις μεγεθών σε διαφορετικά αδρανειακά συστήματα. Το πιο ενδιαφέρον όμως είναι η ίδια η αναλλοιώτητα αυτή. Γενικά τα αναλλοίωτα μεγέθη έχουν μεγάλη σημασία στη σχετικότητα και είναι αυτά τα μεγέθη που μας επιτρέπουν ουσιαστικά να κάνουμε φυσική. Ας επιστρέψουμε στο μήκος της κοσμικής γραμμής. Έστω ότι αυτή η κοσμική γραμμή είναι η κοσμική γραμμή ενός αδρανειακού παρατηρητή. Εγώ μετράω κάποιο μήκος $$\reverse\opaque \Delta s^2$$ στο αδρανειακό σύστημά μου, σύμφωνα με το μέτρο που έχουμε αναφέρει παραπάνω. Τι μετράει όμως ο άλλος αδρανειακός παρατηρητής; Στο δικό του σύστημα το στοιχειώδες μήκος που θα μετρά δεν μπορεί να είναι άλλο από το $$\reverse\opaque \Delta s^2=-c^2\Delta\tau^2$$, όπου "τ" είναι ο δικός του χρόνος, ο ιδιόχρονός του (ο ίδιος ο αδρανειακός παρατηρητής είναι στο κέντρο του συστήματός του και δεν κουνιέται από εκεί). Και αυτό μας οδηγεί σε μια καταπληκτική διαπίστωση. Ο χρόνος που μετρά ένας παρατηρητής είναι το αναλλοίωτο μήκος της κοσμικής γραμμής που διανύει. Ο ιδιόχρονος λοιπόν ενός παρατηρητή είναι το αναλλοίωτο μήκος της κοσμικής γραμμής του. Αυτή η διαπίστωση οδηγεί καταρχήν στο παραπάνω συμπέρασμα, ότι δηλαδή "ο χρόνος που μετρά ένα ρολόι εξαρτάται από την διαδρομή που ακολουθεί", και κατά δεύτερο στο ότι υπάρχει μια αναλλοίωτη έννοια του χρόνου, αυτή που σχετίζεται με τον ιδιόχρονο [1,2].
Αυτά είναι βασικά πράγματα που μαθαίνει κανείς σε ένα εισαγωγικό μάθημα ειδικής σχετικότητας. Αυτή λοιπόν η βασική έννοια του αναλλοίωτου στοιχειώδους μήκους και της σχέσης του με τον ιδιόχρονο, επεκτείνεται και στην θεωρία της γενικής σχετικότητας. Φυσικά, τα πράγματα στην γενική σχετικότητα είναι πιο περίπλοκα (για τις ιδιαιτερότητες και τις διαφορές ανάμεσα στην ειδική και στην γενική σχετικότητα μπορεί να δει κανείς την κουβέντα στα 1, 2, 3 και 4), αλλά τα πράγματα για τις συγκεκριμένες γεωμετρικές έννοιες δεν διαφοροποιούνται σε σχέση με αυτά που είπαμε εδώ. Κάποιος θα μπορούσε να αναρωτηθεί ακόμα, τι μπορεί να συμβαίνει με την εισαγωγή της κβαντομηχανικής στο παιχνίδι και αν αλλάζουν τότε τα πράγματα. Αλλά και πάλι, η εικόνα που έχουμε σχηματίσει μέχρι εδώ δεν αλλάζει σε ότι αφορά την μέχρι τώρα γνωστή φυσική, αφού και στην περίπτωση κβαντικών συστημάτων, η θεωρία που τα περιγράφει είναι η κβαντική θεωρία πεδίου, η οποία χρησιμοποιεί τον χωροχρόνο της ειδικής σχετικότητας για να περιγράψει την εξέλιξη των συστημάτων. Έτσι, χωρίς να μπω σε λεπτομέρειες, ένα κβαντικό σύστημα (ένα ηλεκτρόνιο για παράδειγμα) περιγράφεται από μία κυματοσυνάρτηση η οποία όμως εξελίσσεται με βάση τον ιδιόχρονο που σχετίζεται με αυτό το σύστημα [2]. Με λίγα λόγια, για την μέχρι τώρα διατυπωμένη φυσική, οι παραπάνω έννοιες είναι γενικές και εφαρμόζονται παντού.
Στο σημείο αυτό θα σταματήσω για τώρα. Μέχρι εδώ μιλήσαμε για τον χρόνο στην ειδική σχετικότητα, αλλά μας μένει ακόμα να μιλήσουμε πιο αναλυτικά για τον χρόνο στη γενική σχετικότητα και στην κοσμολογία. Στη γενική σχετικότητα θα δούμε πως η καμπύλωση του χωροχρόνου αλλάζει ποσοτικά τα πράγματα, αλλά όχι ποιοτικά. Θα συζητήσουμε κάποια φαινομενικά παράδοξα και προβλήματα με τον χρόνο και πως αυτά λύνονται. Όλα αυτά τελικά θα μας οδηγήσουν στην έννοια ενός καθολικού χρόνου στην κοσμολογία και το καθαρό και αναλλοίωτο νόημα του ως το χωροχρονικό μήκος των παρατηρητών που βρίσκονται σε ηρεμία μέσα στο σύμπαν, δηλαδή των παρατηρητών που είναι τοπικά ακίνητοι και τους συμπαρασύρει η διαστολή του σύμπαντος.
(to be continued...)
-----------------------
Update: Αξίζει να προσθέσω δύο αναφορές σχετικές με την συζήτηση. Είναι δύο εργασίες στο περιοδικό Science στις οποίες παρουσιάζεται η πειραματική επιβεβαίωση όσων αναφέρονται παραπάνω.
[1] Chou et al., Optical Clocks and Relativity, 2010 Science 329 1630-1633.
[2] Shau-Yu Lan1 et al., A Clock Directly Linking Time to a Particle's Mass, 2013 Science (early view)
Την εκπομπή της ΕΤ3, «Το Σύμπαν που Αγάπησα», την γνωρίζει ο περισσότερος κόσμος. Είναι ίσως η πιο γνωστή επιστημονική σειρά ντοκιμαντέρ της Ελληνικής τηλεόρασης, με πολλούς "φανατικούς" οπαδούς, που έχει δεχθεί και βραβεία. Ιδιαιτερότητα της εκπομπής είναι ότι οι ίδιοι οι παρουσιαστές είναι μέλη της πανεπιστημιακής κοινότητας και συγκεκριμένα είναι ο αναπληρωτής καθηγητής Στράτος Θεοδοσίου και ο επίκουρος καθηγητής Μάνος Δανέζης.
Η βασική θεματολογία της εκπομπής είναι γύρω από θέματα σχετικά με την Αστροφυσική γενικά και ειδικότερα την Κοσμολογία, αλλά και τις σύγχρονες φυσικές θεωρίες όπως είναι για παράδειγμα η θεωρία της Σχετικότητας. Η εκπομπή ακόμα πραγματεύεται και ζητήματα Φιλοσοφίας και Ιστορίας της Επιστήμης. Τα τελευταία δεν θα με απασχολήσουν στο συγκεκριμένο post, αν και έχω και εκεί τους προβληματισμούς μου.
Το θέμα που θα με απασχολήσει, έχει να κάνει και με την ορθότητα της παρουσίασης μίας αρκετά βασικής επιστημονικής έννοιας τόσο συνολικά όπως την συναντάμε στη φυσική όσο και ειδικότερα όπως την συναντάμε στην Κοσμολογία. Δηλαδή θα ασχοληθώ και με την ορθότητα της παρουσίασης στα πλαίσια της εκπομπής «Το Σύμπαν που Αγάπησα», της έννοιας του χρόνου στην φυσική γενικά και στην Κοσμολογία ειδικότερα.
Ίσως θα πρέπει να επισημάνω ότι το πρόβλημα με την συγκεκριμένη εκπομπή, δεν είναι μόνο η λάθος παρουσίαση των σχετικών με τον χρόνο και την Κοσμολογία, αλλά και ένα πλήθος άλλων παρόμοιων σφαλμάτων και παρανοήσεων που οδηγούν σε διάφορα "μονοπάτια" ενώ παρουσιάζονται ως δεδομένη επιστημονική γνώση, με την "βούλα" κιόλας δύο καθηγητών Αστροφυσικής του πανεπιστημίου της Αθήνας. Φυσικά αυτό το θέμα είναι ακόμα πιο πλατύ και δύσκολο και περιλαμβάνει ένα ευρύτερο φάσμα περιπτώσεων "επιστημονικής παραπληροφόρησης" από "ειδικούς" και μη και δεν θα ασχοληθώ περισσότερο εδώ.
Ξεκινάμε λοιπόν με το θέμα του χρόνου στην Κοσμολογία. Παρακάτω παραθέτω δύο σχετικά βίντεο. Το πρώτο είναι απόσπασμα από την ίδια την εκπομπή και συγκεκριμένα ένα επεισόδιο του 3ου κύκλου, ενώ το δεύτερο είναι από μία συνέντευξη, όπου παρουσιάζεται η αντίληψη των δύο καθηγητών για τον χρόνο και την μέτρησή του, στα πλαίσια της κοσμολογίας του Big Bang. Όπως φαίνεται στο δεύτερο βίντεο, με τις απόψεις αυτές που παρουσιάζονται, μάλλον συμφωνεί και ο κ. Αγγελόπουλος, τότε πρόεδρος της Ένωσης Ελλήνων Φυσικών και αναπληρωτής καθηγητής του τομέα Πυρηνικής Φυσικής του πανεπιστημίου Αθηνών.
Απόσπασμα από την εκπομπή της ΕΤ3 «Το Σύμπαν που Αγάπησα», 3ος κύκλος, επεισόδιο 11 με τίτλο, «Η ιστορία του Σύμπαντος». Το απόσπασμα περιγράφει το γιατί κατά τους παρουσιαστές της εκπομπής, αναπληρωτή καθηγητή Στράτο Θεοδοσίου και επίκουρο καθηγητή Μάνο Δανέζη, ο χρόνος στην κοσμολογία δεν έχει νόημα και γιατί η έννοια της ηλικίας του Σύμπαντος είναι ένα χωρίς ουσία κατασκεύασμα. Τη θέση τους αυτή τη στηρίζουν στην υπόθεση ότι η καμπυλότητα του σύμπαντος αλλάζει ανάλογα με την πυκνότητα της ύλης μέσα του και άρα αφού αλλάζει η καμπυλότητα, αλλάζει και η διάρκεια της μονάδας του χρόνου, για παράδειγμα του ενός δευτερολέπτου. Έτσι η εκτίμηση της όποιας ηλικίας του σύμπαντος στερείται νοήματος αφού αθροίζονται δευτερόλεπτα διαφορετικής διάρκειας. Τα παραπάνω τα διατυπώνουν στα πλαίσια της κλασσικής FRW κοσμολογίας (μοντέλο Big Bang).
Η ηλικία του Σύμπαντος -- Ο Χρόνος στην κοσμολογία
Δανέζης για τον χρόνο στην Κοσμολογία
Για όποιον βαρέθηκε να δει τα βίντεο, η άποψη για τον χρόνο συνοψίζεται στην περιγραφή του 1ου βίντεο από το YouTube, που παραθέτω παραπάνω.
Ωραία. Για να απαντηθεί το θέμα που τίθεται, θα πρέπει να τα πάρουμε τα πράγματα λίγο από την αρχή. Να ξεκινήσουμε δηλαδή να συζητάμε για το τι είναι ο χρόνος και ποια η σημασία του, στα πλαίσια της ειδικής σχετικότητας αρχικά και της γενικής σχετικότητας στη συνέχεια. Το μόνο που θα χρειαστεί ως δεδομένο στην όλη συζήτηση, είναι μια βασική αίσθηση γεωμετρίας.
Τι είναι λοιπόν ο χωροχρόνος; Για έναν φυσικό (δηλαδή με άλλα λόγια, για κάποιον που θέλει να κάνει φυσική, δηλαδή να μετρήσει, να παρατηρήσει και να υπολογίσει πράγματα), ο χωροχρόνος είναι ένα σύνολο από «γεγονότα». Όπως το λέει πολύ όμορφα ο R. Geroch (“General Relativity from A to B”, Chicago Press), ένα γεγονός είναι το σκάσιμο μίας κροτίδας ή ένα χτύπημα των δαχτύλων. Ένα «γεγονός» λοιπόν είναι κάτι περιορισμένο στον χώρο και τον χρόνο, το ισοδύναμο ενός μαθηματικού σημείου. Έτσι λοιπόν ο χωροχρόνος αποτελείται από γεγονότα. Ένα πιο «φυσικό» παράδειγμα γεγονότος, είναι η σκέδαση ενός ηλεκτρονίου από ένα φωτόνιο. Η στιγμή της σκέδασης είναι ένα γεγονός. Αντιθέτως, το ίδιο το ηλεκτρόνιο, δεν είναι «γεγονός», αφού αποτελεί κάτι που έχει έκταση, αν όχι στον χώρο τουλάχιστον στον χρόνο. Και εδώ ερχόμαστε στο δεύτερο βασικό συστατικό του χωροχρόνου, τις «κοσμικές γραμμές». Κάθε σωματίδιο, αποτελεί και μία κοσμική γραμμή που εκτείνεται στον χρόνο. Για μία τέτοια κοσμική γραμμή, αν προσδιορίσουμε ένα γεγονός επάνω της, τότε μπορούμε να μιλήσουμε για το «μέλλον» και το «παρελθόν» αυτού του γεγονότος, κατά μήκος της κοσμικής γραμμής. Σε αυτή τη φάση τις έννοιες «μέλλον» και «παρελθόν», τις αναφέρω κάπως αυθαίρετα, αφού δεν έχουμε μιλήσει για το τι σημαίνει ο χρόνος, πράγμα που θα κάνω παρακάτω.
Έτσι λοιπόν, τα βασικά συστατικά του χωροχρόνου είναι τα γεγονότα και οι κοσμικές γραμμές. Με αυτά τα συστατικά και μόνο μπορούμε να μιλήσουμε για χωροχρόνο, χωρίς να χρειάζεται να βάλουμε στη συζήτηση πράγματα όπως «συστήματα συντεταγμένων» και διάφορα άλλα τέτοια. Φυσικά, εμείς δεν είμαστε ικανοποιημένοι μόνο με αυτό. Το ζητούμενο, προκειμένου να κάνει κανείς φυσική, είναι να μιλήσει για την σχέση ανάμεσα σε γεγονότα, δηλαδή να μπορεί να απαντήσει σε ερωτήσεις του τύπου, «το γεγονός Α συμπίπτει με το γεγονός Β;», «το γεγονός Α συνέβη πριν το γεγονός Β;» και διάφορες άλλες τέτοιες ερωτήσεις.
Άρα, εδώ τίθεται το ζήτημα της μέτρησης. Πώς μετράμε στη σχετικότητα ότι έχει σχέση με τα γεγονότα που μας ενδιαφέρουν; Η απάντηση είναι, «μετράμε με τον απλούστερο δυνατό τρόπο, δηλαδή με ράβδους και ρολόγια». Η υλοποίηση αυτής της μετρητικής διαδικασίας είναι ο «παρατηρητής». Ο παρατηρητής, δηλαδή είναι εν γένει μια ιδανική μετρητική συσκευή, εφοδιασμένη με ρολόγια και ράβδους, με τα οποία μετρά χρόνο και αποστάσεις. Μια καλή οπτικοποίηση ενός παρατηρητή είναι αυτή που δίνουν οι Taylor και Wheeler ("Spacetime Physics", W.H.Freeman) όπου ο παρατηρητής είναι ένα πλέγμα από ράβδους και ρολόγια, όπου κάθε ράβδος έχει κάποιο συγκεκριμένο μήκος και σε κάθε κόμβο του πλέγματος υπάρχει ένα ρολόι. Έτσι σε κάθε γεγονός αποδίδουμε κάποιο χρόνο και κάποια θέση σύμφωνα με την παρακάτω διαδικασία: για κάποιο γεγονός που συμβαίνει, του αποδίδουμε τον χρόνο που καταγράφει το κοντινότερο ρολόι στο γεγονός, ενώ για την θέση, του αποδίδουμε την θέση του ίδιου ρολογιού. Ακόμα δεν έχουμε καθορίσει τι είναι αυτός ο χρόνος ή η θέση, αλλά θα το κάνουμε σύντομα. Φυσικά, ανάλογα με την ακρίβεια που θέλουμε, μπορούμε να κάνουμε τα μήκη των ράβδων οσοδήποτε μικρά, καθώς και την ακρίβεια των ρολογιών μας, έτσι ώστε να καλύπτουμε όσο πυκνά θέλουμε όλον τον χώρο και τον χρόνο. Από την παραπάνω εικόνα φαίνεται ότι σε κάθε παρατηρητή, αντιστοιχεί και ένα σύστημα αναφοράς. Η ειδική κλάση των παρατηρητών και των συστημάτων που κινούνται ελεύθερα, χωρίς να επιταχύνονται ή να ασκούνται δυνάμεις επάνω τους, ονομάζονται αδρανειακοί παρατηρητές και αδρανειακά συστήματα αντίστοιχα. Αυτά τα συστήματα όπως τα περιγράψαμε ως πλέγμα, αποτελούν ουσιαστικά και ένα τύπο συστήματος συντεταγμένων, όπου για παράδειγμα ένα γεγονός αποκτά τις συντεταγμένες θέσης, ως προς ένα σημείο αναφοράς, του πλησιέστερου ρολογιού, δηλαδή 3 ράβδους κατά μήκος του ενός άξονα, 5 ράβδους κατά μήκος του άλλου άξονα και 1 ράβδο κατά μήκους του 3ου άξονα (θέση x,y,z) ενώ έχει και την καταγραφή ενός χρόνου από το αντίστοιχο ρολόι (χρόνος t). Πριν όμως προχωρήσουμε περισσότερο στις συντεταγμένες, πρέπει να επιστρέψουμε στο τι είναι ο χρόνος που μετράνε τα ρολόγια και η απόσταση που μετράνε οι ράβδοι.

Ο χρόνος και ο χώρος, είπαμε παραπάνω, ότι μετριέται με ρολόγια και ράβδους. Υπάρχει όμως το ερώτημα, μήπως κρύβεται κάτι περισσότερο πίσω από αυτό; Η απάντηση είναι όχι. Όλη η ουσία νομίζω ότι μπορεί να αποδοθεί με την παρακάτω διατύπωση από το πολύ καλό εκλαϊκευτικό βιβλίο του Hermann Bondi, «Σχετικότητα και κοινή λογική», που έχει μεταφραστεί από τις εκδόσεις Τροχαλία, η οποία είναι:
«Χρόνος είναι αυτό που μετρά ένα ρολόι. Αυτός είναι ο σωστός τρόπος να βλέπουμε τα πράγματα. Μία ποσότητα, όπως ο χρόνος ή οποιοδήποτε άλλο φυσικό μέγεθος, δεν υπάρχει κατά τρόπο αφηρημένο. Δεν έχει κανένα νόημα να συζητάμε για κάτι παρά μόνο όταν καθορίσουμε το πώς θα το μετράμε. Ο καθορισμός της μεθόδου μέτρησής του είναι ο μόνος σίγουρος τρόπος για να αποφύγουμε τις χωρίς νόημα συζητήσεις.»
Η διατύπωση αυτή, κάνει απόλυτα σαφές τι σημαίνει χρόνος και χώρος. Χρόνος είναι αυτό που μετρά το ρολόι μου και χώρος είναι αυτό που μετρά η ράβδος μου. Το ίδιο ακριβώς πράγμα ξεκαθαρίζει και ο Einstein στην πρώτη εκείνη εργασία του 1905, «Επί της Ηλεκτροδυναμικής των Κινούμενων Σωμάτων». Συγκεκριμένα, παραθέτω από την μετάφραση του Θάνου Χριστακόπουλου, από τις εκδόσεις Τροχαλία, «Η ειδική θεωρία της Σχετικότητας (Τα πρωτότυπα άρθρα)»,
«Η θεωρία που πρόκειται να αναπτυχθεί, βασίζεται – όπως και όλη η ηλεκτροδυναμική – στην κινηματική του στερεού σώματος, από τη στιγμή που οι ισχυρισμοί οποιασδήποτε τέτοιας θεωρίας συνδέονται με τις σχέσεις μεταξύ στερεών σωμάτων (συστημάτων συντεταγμένων), ρολογιών και ηλεκτρομαγνητικών διαδικασιών.»
Η αναφορά αυτή του Einstein, εμφανίζει και τα ηλεκτρομαγνητικά φαινόμενα ως πρωταρχικής σημασίας για την θεωρία της σχετικότητας και αυτό οφείλεται στον σημαντικό ρόλο που παίζει η ταχύτητα του φωτός, ως μία σταθερά της ηλεκτρομαγνητικής θεωρίας (σε αυτό θα αναφερθούμε παρακάτω).
Η έμφαση που δίνεται σε αυτό το σημείο στο γεγονός ότι ο χρόνος για έναν παρατηρητή είναι αυτό που μετρά το ρολόι του (όπου φυσικά αυτό μπορεί να το δει κανείς σε οποιοδήποτε βιβλίο σχετικότητας και αν ανοίξει), έρχεται σε σαφή αντίθεση με αυτά που διατυπώνονται στα παραπάνω βίντεο ειδικά και στο σύνολο των συγκεκριμένων εκπομπών γενικά. Παρακάτω θα γίνει ακόμα πιο ξεκάθαρη η σημασία της διατύπωσης ότι «ο χρόνος ενός παρατηρητή είναι αυτός που μετράει το ρολόι του» και της καθολικότητας αυτής της πρότασης.
Ωραία, είπαμε μέχρι τώρα ότι τα θεμελιώδη συστατικά του χωροχρόνου είναι τα γεγονότα και οι κοσμικές γραμμές, όπου παράδειγμα των τελευταίων είναι τα στοιχειώδη σωματίδια όπως τα ηλεκτρόνια και τα φωτόνια, ενώ ορίσαμε και τι συνιστά μέσα στο χωροχρόνο ένας παρατηρητής, πως αυτός καθορίζει ένα σύστημα αναφοράς και ότι οι μετρήσεις σε αυτό το σύστημα γίνονται με ράβδους σταθερού μήκους και ρολόγια που εκτίνονται παντού γύρω του.
Το επόμενο ερώτημα είναι, πως ακριβώς μετράνε τα ρολόγια το χρόνο και πως ακριβώς μετράνε οι ράβδοι τα μήκη. Υπάρχει κάποιο ρολόι που να είναι καλύτερο από το άλλο; Και ποια είναι η σχέση του χρόνου που μετρά ένα ρολόι εδώ με το χρόνο που μετρά ένα ρολόι κάπου αλλού; Με άλλα λόγια, ποιος είναι ο καλύτερος φυσικός μηχανισμός για να μετρήσουμε τον χρόνο, αν υπάρχει αυτός, ή ποιος είναι ο καλύτερος φυσικός μηχανισμός για να μετρήσουμε αποστάσεις, αν υπάρχει αυτός, και τέλος, πως ακριβώς συγχρονίζουμε τα διάφορα ρολόγια μεταξύ τους. Ειδικά το τελευταίο αποτελεί και ιδιαιτέρως σημαντικό θέμα, αφού ακόμα και η απόδοση κάποιας χρονικής στιγμής σε ένα γεγονός είναι ζήτημα της σύγκρισης της στιγμής που έγινε το γεγονός με τον χρόνο που έδειξε κάποιο ρολόι, δηλαδή είναι ζήτημα συγχρονισμού.
Σε αυτό το σημείο, πρέπει να επισημάνουμε ότι η καθημερινή μας εμπειρία της μέτρησης του χρόνου με ρολόγια που μετράνε δευτερόλεπτα και της μέτρησης των αποστάσεων με χάρακες που μετράνε μέτρα, συσκοτίζει την ενότητα που υπάρχει ανάμεσα στον χώρο και τον χρόνο. Δηλαδή δημιουργεί μια φαινόμενη ποιοτική διαφοροποίηση ανάμεσα στα δύο. Το πρόβλημα αυτό έρχεται να το ξεπεράσει η μία από τις δύο αρχές της ειδικής σχετικότητας, η αρχή της σταθερότητας της ταχύτητας του φωτός. Και ο τρόπος που το κάνει αυτό έχει αρκετό ενδιαφέρον.
Εδώ αξίζει να αναφέρουμε την παραβολή με τις δύο σχολές τοπογράφων που παρουσιάζουν οι Taylor και Wheeler (“Spacetime Physics”, W.H.Freeman), η οποία μπορεί να μας διδάξει πολλά σημαντικά πράγματα για τις βάσεις της ειδικής σχετικότητας. Θα παραθέσω την παραβολή σε μετάφραση (σχετικά ελεύθερη):
«Μια φορά και έναν καιρό, υπήρχε ένας τοπογράφος που ανήκε στη σχολή των Τοπογράφων της Ημέρας, ο οποίος κατέγραψε όλη τη γη του Βασιλιά. Για να καθορίσει τις διευθύνσεις Βορά-Νότου και Ανατολής-Δύσης, χρησιμοποιούσε μία μαγνητική πυξίδα. Οι θέσεις μετριόνταν από το κέντρο της πλατείας της πόλης. Στην διεύθυνση Ανατολής-Δύσεις οι θέσεις μετριόνταν σε μέτρα (x σε μέτρα). Στην διεύθυνση Βορά-Νότου που ήταν «ιερή» οι θέσεις μετριόνταν σε μίλια (y σε μίλια). Η καταγραφή που είχε κάνει αυτός ο τοπογράφος ήταν πολύ ακριβής και πλήρης.
Υπήρχε και ένας άλλος τοπογράφος, που ανήκε στη σχολή των Τοπογράφων της Νύχτας, ο οποίος είχε καταγράψει και αυτός όλη τη γη του Βασιλιά. Η σχολή της Νύχτας, για να καθορίσει τις διευθύνσεις Βορά-Νότου και Ανατολής-Δύσης, χρησιμοποιούσε τον πολικό αστέρα. Ο τοπογράφος της σχολής της Νύχτας μετρούσε και εκείνος τις θέσεις στη διεύθυνση Ανατολής-Δύσης σε μέτρα και τις θέσεις στη διεύθυνση Βορά-Νότου σε μίλια (x’ σε μέτρα, y’ σε μίλια).
Κάποτε εμφανίστηκε ένας μαθητής της τοπογραφίας, που αποφάσισε να παρακολουθήσει και τις δύο σχολές. Έτσι έμαθε και την μέθοδο των Τοπογράφων της Ημέρας και την μέθοδο των Τοπογράφων της Νύχτας. Ο μαθητής, διδασκόμενος και τις δύο μεθόδους προσπαθούσε να βρει μία σχέση ανάμεσα στις καταγραφές των θέσεων ώστε να μπορέσει να συνδέσει τα αποτελέσματα μεταξύ τους. Έτσι κάποια στιγμή αποφάσισε να μετατρέψει τις μετρήσεις στην «ιερή» διεύθυνση Βορά-Νότου από μίλια σε μέτρα, πολλαπλασιάζοντας με μία σταθερά αναλογίας k. Κάνοντας αυτή τη μετατροπή, ανακάλυψε ότι η απόσταση των πυλών της πόλης από το κέντρο της πλατείας από όπου ξεκίναγαν οι μετρήσεις, δηλαδή η ποσότητα $$\reverse\opaque \sqrt{(x)^2+(ky)^2}$$, με βάση τις μετρήσεις των Τοπογράφων της Ημέρας, συνέπιπτε με την απόσταση που βασιζόταν στις μετρήσεις των Τοπογράφων της Νύχτας, $$\reverse\opaque \sqrt{(x')^2+(ky')^2}$$. Την ανακάλυψή του αυτή, ο μαθητής την ονόμασε «Αρχή του Αναλλοίωτου της Απόστασης».»
Αυτή η παραβολή μας λέει πολλά ενδιαφέροντα πράγματα. Το πρώτο και σημαντικότερο ίσως, μας το λέει η αναφορά της «ιερής» διεύθυνσης Βορά-Νότου, η οποία μετριέται με άλλες μονάδες μέτρησης, δηλαδή μίλια, που σχετίζονται με μία σταθερά αναλογίας k με τις μονάδες μέτρησης στην διεύθυνση Ανατολής-Δύσης. Αυτό είναι σαφής αναφορά στον χρόνο και την μέτρησή του σε δευτερόλεπτα, ενώ η σταθερά αναλογίας αναφέρεται στην ταχύτητα του φωτός. Με δεδομένη την αρχή της σταθερότητας της ταχύτητας του φωτός, μπορούμε να θεωρήσουμε αυτή την ταχύτητα ως σταθερά αναλογίας ανάμεσα στον χρόνο και τον χώρο, αφού ο λόγος $$\reverse\opaque s / t$$ υποδεικνύει κάποια ταχύτητα, ενώ ο λόγος $$\reverse\opaque s / c$$ υποδεικνύει κάποιο χρόνο και από την άλλη το γινόμενο $$\reverse\opaque c t$$ υποδεικνύει κάποια απόσταση. Θεωρώντας λοιπόν την ταχύτητα του φωτός ως παγκόσμια σταθερά, μπορούμε να μετρήσουμε την απόσταση σε δευτερόλεπτα ή τον χρόνο σε μέτρα, με τον ίδιο τρόπο περίπου που στην επιφάνεια της Γης, σε κάποιο συγκεκριμένο τόπο όπου η επιτάχυνση της βαρύτητας είναι σταθερή, μετράμε το βάρος μας (που είναι δύναμη) σε κιλά. Πρακτικά πως μπορούμε να το κάνουμε όμως αυτό; Δηλαδή, πως θα φτιάξω εγώ πρακτικά τα ρολόγια ή τις ράβδους που αναφέραμε παραπάνω, που αποτελούν τον παρατηρητή και το σύστημα του;
Αν βάλω ως βάση μου τις στέρεες ράβδους, τότε μπορώ να μετράω τον χρόνο μου σε μέτρα με το παρακάτω ρολόι. Βάζω δύο καθρέφτες στα άκρα μίας ράβδου, μήκους μισού μέτρου και στέλνω έναν παλμό από τον ένα καθρέφτη, προς τον άλλον. Ο παλμός θα φτάσει στον άλλον καθρέφτη, όπου θα ανακλαστεί και θα επιστρέψει στον πρώτο καθρέφτη. Κάθε φορά που αυτός ο κύκλος θα επαναλαμβάνετε, το φως θα έχει διανύσει ακόμα ένα μέτρο, άρα θα έχει περάσει χρόνος ίσος με ένα μέτρο φωτός ή $$\reverse\opaque t=\frac{1m}{c}=\frac{1}{3}\times 10^{-8}s$$. Σε κάθε «τικ», το ρολόι μας θα μετρά τόσο χρόνο.
Αντίστοιχα, μπορώ να βάλω ως βάση τον χρόνο που καταγράφει κάποιο ρολόι. Έτσι, μετρώντας τον χρόνο που κάνει ένας παλμός φωτός για να πάει μέχρι κάποιο σημείο, να ανακλαστεί και να επιστρέψει (υποτυπώδες συσκευή ραντάρ), μπορώ να υπολογίσω την απόσταση σε δευτερόλεπτα ή αλλιώς για δύο δευτερόλεπτα που θα κάνει το φως να πάει και να έρθει, η απόσταση θα είναι $$\reverse\opaque x = c \times 1s =3\times 10^{8}m$$. Φυσικά, αυτή η απόσταση είναι τεράστια. Αυτός είναι και ο τρόπος που μετράμε αποστάσεις στην Αστρονομία, όπου οι συμβατικές μονάδες είναι πολύ μικρές. Έτσι, εκεί έχουμε το έτος φωτός. Φυσικά μπορούμε να μικρύνουμε όσο χρειάζεται την μονάδα μέτρησης του χρόνου, ώστε να μπορούμε να μετρήσουμε και μικρότερες αποστάσεις.
Από τα παραπάνω, φαίνεται ότι το αξίωμα της σταθερότητας της ταχύτητας του φωτός μας δίνεις την δυνατότητα να αντιμετωπίσουμε με τον ίδιο τρόπο και τον χώρο και τον χρόνο.
Κάποιος όμως και πάλι θα μπορούσε να επιμείνει στο ερώτημα του πως είμαστε σίγουροι ότι όλα τα ρολόγια, θα κρατάνε τον ίδιο ρυθμό όπου και να τα βάλουμε ή πως είμαστε σίγουροι ότι όλες οι ράβδοι θα έχουν το ίδιο μήκος όπου και να τις βάλουμε; Αρχικά, πρέπει να πούμε ότι μιλάμε για «ιδανικά ρολόγια» και «ιδανικές ράβδους» (ιδανικά στερεά σώματα δηλαδή). Ακριβώς ιδανικό ρολόι και ράβδος δεν υπάρχει στην φύση, αλλά μπορούμε να το προσεγγίσουμε σχεδόν όσο καλά θέλουμε. Για παράδειγμα, αρχικά τον χρόνο σε μεγάλη κλίμακα τον μετράγαμε με την αλλαγή των εποχών και σε μικρότερη κλίμακα με την αλλαγή της θέσης του Ήλιου. Αυτό ήταν ένα καλό ρολόι για τις τότε απαιτήσεις. Αργότερα, μετράγαμε το χρόνο με κλεψύδρες και κεριά για μεγαλύτερη ακρίβεια. Από την εποχή του Γαλιλαίου, μετράμε τον χρόνο με εκκρεμή, που έχουν την ικανότητα να κρατάνε με σχετικά καλή ακρίβεια την περίοδό τους σταθερή. Σήμερα, πετυχαίνουμε, σε εμπορικές χρήσεις, πολύ καλή ακρίβεια στη μέτρηση του χρόνου, μετρώντας τις ταλαντώσεις ενός κρύσταλλου χαλαζία, ενώ για ακόμα μεγαλύτερη ακρίβεια χρησιμοποιούνται τα ατομικά ρολόγια των οποίων η λειτουργία στηρίζεται στην μέτρηση της συχνότητας της μικροκυματικής ακτινοβολίας που εκπέμπουν ή απορροφούν κάποια άτομα Κεσίου κατά την αποδιέγερση ή την διέγερσή τους. Έτσι ουσιαστικά, επιλέγοντας το κατάλληλο φυσικό σύστημα, μπορούμε να αυξήσουμε μέχρι το επιθυμητό επίπεδο την ακρίβεια της μέτρησης του χρόνου, μετρώντας τις «ταλαντώσεις» του αντίστοιχου συστήματος. Εδώ βλέπουμε ουσιαστικά ότι και πάλι το φως και συγκεκριμένα η συχνότητά του αποτελεί ένα μέτρο για την μέτρηση του χρόνου (δεδομένης της σταθερότητας της ταχύτητάς του στο κενό). Κάτι ανάλογο ισχύει και για τα μήκη των ράβδων που μπορούμε να χρησιμοποιήσουμε, όπου και αυτά εξαρτώνται από τις ταλαντώσεις των ατόμων που αποτελούν κάποιο στερεό σώμα και είναι διατεταγμένα σε κάποιο πλέγμα. Έτσι, μία από τις πρώτες συμβάσεις για την μέτρηση του μήκους ήταν η χρήση πρότυπων ράβδων κατασκευασμένων από υλικό που είχε την ικανότητα να μην αλλάζει πολύ το μήκος του με την αλλαγή της θερμοκρασίας. Αργότερα και αυτό το πρότυπο αντικαταστάθηκε από ένα πρότυπο βασισμένο στο μήκος κύματος της ακτινοβολίας μίας φασματικής γραμμής που εκπέμπει το άτομο του Κρυπτού. Δηλαδή και πάλι μετράμε τα μήκη με την βοήθεια του φωτός μέσω κάποιας ενεργειακής μετάβασης ενός ατόμου. Έτσι το μόνο που μας μένει για να έχουμε πανομοιότυπες «ράβδους» και «ρολόγια» είναι να χρησιμοποιήσουμε τα αντίστοιχα άτομα ως πρότυπα. Ναι, αλλά αυτά τα άτομα θα μας δίνουν το ίδιο αποτέλεσμα στην μέτρηση του χώρου και του χρόνου όπου και να τα τοποθετήσουμε; Η απάντηση είναι, ναι. Αυτό μας το εξασφαλίζει η δεύτερη βασική αρχή της θεωρίας της σχετικότητας, η αρχή της αναλλοιώτητας των φυσικών νόμων, δηλαδή η αρχή που λέει ότι οι φυσικοί νόμοι πρέπει να είναι η ίδιοι παντού και να δίνουν το ίδιο αποτέλεσμα για ένα πείραμα, οπουδήποτε ή οποτεδήποτε και αν αυτό πραγματοποιηθεί.
Έτσι, οι δύο βασικές αρχές της θεωρίας της σχετικότητας, μας επιτρέπουν να μετράμε τα μήκη και τους χρόνους παντού μέσα στο σύστημά μας, δηλαδή με λίγα λόγια μας επιτρέπουν την κατασκευή αυτού του πράγματος που είπαμε ιδανικό παρατηρητή.
Και τώρα ερχόμαστε στο άλλο μεγάλο θέμα που αφορά το πώς μετράμε οπουδήποτε μέσα στο σύστημά μας. Έστω ότι έχουμε απλώσει τα ρολόγια μας και τις ράβδους μας σε όλο το χώρο. Θα πρέπει να ρυθμίσω τα ρολόγια που έχω τοποθετήσει, έτσι ώστε να δείχνουν τον «σωστό» χρόνο, δηλαδή θα πρέπει να συγχρονίσω όλα τα ρολόγια μεταξύ τους. Και πάλι, ο συγχρονισμός των ρολογιών γίνεται με την βοήθεια του φωτός. Έστω ότι έχουμε το δικό μας ρολόι και ένα ρολόι σε κάποια απόσταση από εμάς που βρισκόμαστε στο κέντρο του συστήματος (στο κέντρο των αξόνων x,y,z). Στέλνουμε έναν παλμό φωτός προς το άλλο ρολόι την στιγμή $$\reverse\opaque t_1=t_0-\Delta t$$. Αν ο παλμός αυτός ανακλαστεί και φτάσει πίσω σε εμάς την στιγμή $$\reverse\opaque t_2=t_0+\Delta t$$, τότε λέμε ότι την στιγμή που ανακλάστηκε ο παλμός στο άλλο ρολόι, αυτό θα πρέπει να δείχνει χρόνο $$\reverse\opaque t_0$$ προκειμένου τα δύο ρολόγια να είναι συγχρονισμένα. Έτσι, εφαρμόζοντας μία τέτοια διαδικασία σε κάθε απομακρυσμένο ρολόι, μπορούμε να συγχρονίσουμε όλα τα ρολόγια στο σύστημα αναφοράς μας. Η διαδικασία του συγχρονισμού βασίζεται και αυτή στο γεγονός ότι η ταχύτητα του φωτός είναι σταθερή και άρα ο χρόνος που χρειάζεται το φως για να πάει και να έρθει προς και από το άλλο ρολόι που είναι ακίνητο σε κάποια απόσταση από εμάς είναι σταθερός. Έτσι η στιγμή της ανάκλασης είναι στη μέση αυτού του χρονικού διαστήματος. Εδώ μπορεί κάποιος να αναρωτηθεί, γιατί επιλέγουμε αυτή τη διαδικασία συγχρονισμού και δεν στέλνουμε για παράδειγμα κάποιο τρίτο ρολόι από εδώ εκεί ώστε να συγχρονιστούν τα δύο απομακρυσμένα ρολόγια; Η απάντηση είναι ένα από τα πιο ενδιαφέροντα αποτελέσματα της θεωρίας της σχετικότητας. Ο χρόνος που μετρά ένα ρολόι εξαρτάται από την διαδρομή που ακολουθεί [1,2].
Αυτό μας φέρνει πίσω στην παραβολή με τους τοπογράφους και στην «Αρχή του Αναλλοίωτου της Απόστασης». Μέχρι τώρα έχουμε χρησιμοποιήσει την αρχή της σταθερότητας της ταχύτητας του φωτός για να φέρουμε στην ίδια βάση τον χώρο και τον χρόνο και για να συγχρονίσουμε τα ρολόγια ενός αδρανειακού παρατηρητή, ενώ έχουμε χρησιμοποιήσει την αναλλοιώτητα των φυσικών νόμων για να εξασφαλίσουμε ότι μπορούμε πάντα και παντού να κάνουμε τις μετρήσεις του χρόνου και του μήκους που χρειαζόμαστε. Η ιδέα του αναλλοίωτου της χωχροχρονικής απόστασης μας δίνει τώρα τη δυνατότητα να συγκρίνουμε τις μετρήσεις που πραγματοποιούν διαφορετικοί παρατηρητές σε διαφορετικά αδρανειακά συστήματα, αλλά ακόμα μας δίνει και την δυνατότητα να ορίσουμε τον χρόνο με απόλυτο τρόπο.
Η «Αρχή του Αναλλοίωτου της Απόστασης», όπως την περιγράψαμε στην παραβολή των τοπογράφων, ισχύει και για τα χωροχρονικά μήκη στην ειδική σχετικότητα, όπου αυτή τη φορά έχουμε το χωροχρονικό μέτρο $$\reverse\opaque ds^2=-c^2dt^2+dx^2+dy^2+dz^2$$ να είναι αναλλοίωτο. Αν έχουμε μια κοσμική γραμμή στον χωροχρόνο, μπορούμε τότε να μετρήσουμε το αναλλοίωτο χωροχρονικό μήκος της χρησιμοποιώντας την προηγούμενη σχέση. Το αποτέλεσμα αυτού του υπολογισμού θα είναι μια γεωμετρική ποσότητα την οποία οποιοσδήποτε παρατηρητής και να την μετρήσει θα την βρει να είναι η ίδια. Χρησιμοποιώντας αυτή την αναλλοιώτητα ανάμεσα στην μέτρηση τέτοιων μεγεθών από διαφορετικούς παρατηρητές, μπορεί να οδηγηθεί κανείς στους μετασχηματισμούς του Lorentz που συνδέουν τις μετρήσεις μεγεθών σε διαφορετικά αδρανειακά συστήματα. Το πιο ενδιαφέρον όμως είναι η ίδια η αναλλοιώτητα αυτή. Γενικά τα αναλλοίωτα μεγέθη έχουν μεγάλη σημασία στη σχετικότητα και είναι αυτά τα μεγέθη που μας επιτρέπουν ουσιαστικά να κάνουμε φυσική. Ας επιστρέψουμε στο μήκος της κοσμικής γραμμής. Έστω ότι αυτή η κοσμική γραμμή είναι η κοσμική γραμμή ενός αδρανειακού παρατηρητή. Εγώ μετράω κάποιο μήκος $$\reverse\opaque \Delta s^2$$ στο αδρανειακό σύστημά μου, σύμφωνα με το μέτρο που έχουμε αναφέρει παραπάνω. Τι μετράει όμως ο άλλος αδρανειακός παρατηρητής; Στο δικό του σύστημα το στοιχειώδες μήκος που θα μετρά δεν μπορεί να είναι άλλο από το $$\reverse\opaque \Delta s^2=-c^2\Delta\tau^2$$, όπου "τ" είναι ο δικός του χρόνος, ο ιδιόχρονός του (ο ίδιος ο αδρανειακός παρατηρητής είναι στο κέντρο του συστήματός του και δεν κουνιέται από εκεί). Και αυτό μας οδηγεί σε μια καταπληκτική διαπίστωση. Ο χρόνος που μετρά ένας παρατηρητής είναι το αναλλοίωτο μήκος της κοσμικής γραμμής που διανύει. Ο ιδιόχρονος λοιπόν ενός παρατηρητή είναι το αναλλοίωτο μήκος της κοσμικής γραμμής του. Αυτή η διαπίστωση οδηγεί καταρχήν στο παραπάνω συμπέρασμα, ότι δηλαδή "ο χρόνος που μετρά ένα ρολόι εξαρτάται από την διαδρομή που ακολουθεί", και κατά δεύτερο στο ότι υπάρχει μια αναλλοίωτη έννοια του χρόνου, αυτή που σχετίζεται με τον ιδιόχρονο [1,2].
Αυτά είναι βασικά πράγματα που μαθαίνει κανείς σε ένα εισαγωγικό μάθημα ειδικής σχετικότητας. Αυτή λοιπόν η βασική έννοια του αναλλοίωτου στοιχειώδους μήκους και της σχέσης του με τον ιδιόχρονο, επεκτείνεται και στην θεωρία της γενικής σχετικότητας. Φυσικά, τα πράγματα στην γενική σχετικότητα είναι πιο περίπλοκα (για τις ιδιαιτερότητες και τις διαφορές ανάμεσα στην ειδική και στην γενική σχετικότητα μπορεί να δει κανείς την κουβέντα στα 1, 2, 3 και 4), αλλά τα πράγματα για τις συγκεκριμένες γεωμετρικές έννοιες δεν διαφοροποιούνται σε σχέση με αυτά που είπαμε εδώ. Κάποιος θα μπορούσε να αναρωτηθεί ακόμα, τι μπορεί να συμβαίνει με την εισαγωγή της κβαντομηχανικής στο παιχνίδι και αν αλλάζουν τότε τα πράγματα. Αλλά και πάλι, η εικόνα που έχουμε σχηματίσει μέχρι εδώ δεν αλλάζει σε ότι αφορά την μέχρι τώρα γνωστή φυσική, αφού και στην περίπτωση κβαντικών συστημάτων, η θεωρία που τα περιγράφει είναι η κβαντική θεωρία πεδίου, η οποία χρησιμοποιεί τον χωροχρόνο της ειδικής σχετικότητας για να περιγράψει την εξέλιξη των συστημάτων. Έτσι, χωρίς να μπω σε λεπτομέρειες, ένα κβαντικό σύστημα (ένα ηλεκτρόνιο για παράδειγμα) περιγράφεται από μία κυματοσυνάρτηση η οποία όμως εξελίσσεται με βάση τον ιδιόχρονο που σχετίζεται με αυτό το σύστημα [2]. Με λίγα λόγια, για την μέχρι τώρα διατυπωμένη φυσική, οι παραπάνω έννοιες είναι γενικές και εφαρμόζονται παντού.
Στο σημείο αυτό θα σταματήσω για τώρα. Μέχρι εδώ μιλήσαμε για τον χρόνο στην ειδική σχετικότητα, αλλά μας μένει ακόμα να μιλήσουμε πιο αναλυτικά για τον χρόνο στη γενική σχετικότητα και στην κοσμολογία. Στη γενική σχετικότητα θα δούμε πως η καμπύλωση του χωροχρόνου αλλάζει ποσοτικά τα πράγματα, αλλά όχι ποιοτικά. Θα συζητήσουμε κάποια φαινομενικά παράδοξα και προβλήματα με τον χρόνο και πως αυτά λύνονται. Όλα αυτά τελικά θα μας οδηγήσουν στην έννοια ενός καθολικού χρόνου στην κοσμολογία και το καθαρό και αναλλοίωτο νόημα του ως το χωροχρονικό μήκος των παρατηρητών που βρίσκονται σε ηρεμία μέσα στο σύμπαν, δηλαδή των παρατηρητών που είναι τοπικά ακίνητοι και τους συμπαρασύρει η διαστολή του σύμπαντος.
(to be continued...)
-----------------------
Update: Αξίζει να προσθέσω δύο αναφορές σχετικές με την συζήτηση. Είναι δύο εργασίες στο περιοδικό Science στις οποίες παρουσιάζεται η πειραματική επιβεβαίωση όσων αναφέρονται παραπάνω.
[1] Chou et al., Optical Clocks and Relativity, 2010 Science 329 1630-1633.
[2] Shau-Yu Lan1 et al., A Clock Directly Linking Time to a Particle's Mass, 2013 Science (early view)

31 σχόλια:
Επειδή η φυσική κοιλοπονάει εδώ και πάρα πολύ καιρό μην δίνοντας -ακόμη- νέες απαντήσεις (ακόμα και η ανακοίνωση για το σωματίδιο του Χίγκς με μισή καρδιά έγινε …), βρίσκουν την ευκαιρία διάφοροι, ξεκινώντας από το ίδιο το Πανεπιστήμιο ως καθηγητές ή ως ‘αστροναύτες’ μητροπολίτες της Μεσογαίας (για παράδειγμα) να σπεκουλάρουν αποδομώντας ανεπαισθήτως αυτό που χτίστηκε με κόπους αιώνων.
Η κριτική σας εξαιρετικά ευγενής και μετρημένη (ίσως περισσότερο από όσο θα έπρεπε) και το κείμενό σας χρήσιμο. Ευχαριστώ και καλή χρονιά.
ΥΓ. Ο γιός μου έκανε την διπλωματική του σε έναν από τους δύο. Στην αρχή χάρηκα, όταν όμως κατάλαβα περί τίνος πρόκειται στενοχωρήθηκα πολύ.
Είναι ένα αρκετά περίπλοκο πρόβλημα, το οποίο όμως έχει ως θύματα πρώτα τους φοιτητές μέσα στα αμφιθέατρα και μετά και τον κόσμο πιο έξω. Ελπίζω φέτος να υπάρξει κάποια παραπάνω κινητικότητα στο θέμα, τουλάχιστον σε επίπεδο αντίλογου και ενημέρωσης.
Καλή χρονιά grsail.
Ωραίο άρθρο. Αναρωτιέμαι αν το explicatum "χρόνος" στη φυσική αναφέρεται συχνά σε (μερικώς) διαφορετικό explicandum (έννοια) από εκείνο με την οποία ασχολείται φιλοσοφία ή από εκείνο στο οποίο αναφερόμαστε στην καθημερινότητα μας. Αυτό γιατί αν ήταν απολύτως ταυτόσημες έχω την εντύπωση πως θα προέκυπταν κάποιες λογικές ασυνέπειες.
@epanechnikov
Όχι μόνο ταυτίζονται αγαπητέ αλλά τον θεωρούν και οντότητα με την οποία μπορείς να αλληλεπιδράς (διαστέλλεται, συστέλλεται, κλπ).
Για εμένα και για τον λογική αυτό είναι κλασσική περίπτωση του σφάλματος της πραγμάτωσης (reification fallacy) αλλά για την θεωρητική φυσική φαίνεται ότι αυτές οι πλάνες είναι ασήμαντες λεπτομέρειες.
Υ.Γ. Ωραίο blog έχεις για στατιστικά θέματα.. σε ενδιαφέρει το cointegration analysis;
Έχεις δίκαιο epanechnikov ότι η λέξη χρόνος χρησιμοποιείται με πολλές έννοιες. Υπάρχουν διαφοροποιήσεις τόσο ανάμεσα στο νόημα που μπορεί να έχει στην φιλοσοφία σε σχέση με την φυσική, όσο και στην ίδια τη φυσική όταν χρησιμοποιείται σε διαφορετικό πλαίσιο. Για παράδειγμα είναι άλλο το νόημα του χρόνου ως μια παράμετρος που μετρά την εξέλιξη ενός συστήματος, η οποία μπαίνει στις διαφορικές μας εξισώσεις, είναι άλλο το νόημα του χρόνου ως μια συντεταγμένη στη σχετικότητα (coordinate time) και άλλο στην θερμοδυναμική. Κάθε φορά όμως και σε κάθε πλαίσιο, τουλάχιστον στη φυσική, είναι σαφές για ποιο χρόνο μιλάμε. Πέρα από αυτό, αυτές οι διάφορες έννοιες μπορούν να συνδεθούν μεταξύ τους, για παράδειγμα εδώ ο ιδιόχρονος μπορεί να παίξει τον ρόλο της παραμέτρου που μετρά την εξέλιξη ενός συστήματος ή για να το πω ανάποδα στα φυσικά συστήματα μπορεί να δείξει κανείς ότι αυτή η παράμετρος τελικά είναι ο ιδιόχρονος ή στη θερμοδυναμική περιγραφή ενός σύνθετου συστήματος από την αδρομερή περιγραφή του αναδύεται ένας θερμοδυναμικός χρόνος που συμπίπτει με την Νευτώνεια παράμετρο εξέλιξης. Ο δε ιδιόχρονος μπορεί να συμπίπτει με τον συντεταγμένο χρόνο ή μπορεί να είναι διαφορετικός. Θέλει λίγο προσοχή για να μην μπλέκει τα πράγματα κανείς.
Ο χρόνος για την σχετικότητα είναι μόνο συντεταγμένη;
Ο χρόνος στη σχετικότητα είναι πάντα ο χρόνος που μετρά κάποιος παρατηρητής. Όταν διαλέξουμε κάποια κλάση παρατηρητών ως προς την οποία θα εκφράσουμε τις ποσότητες που μετράμε (δηλαδή όταν διαλέξουμε τους παρατηρητές που κάνουν τις μετρήσεις) τότε λέμε ότι έχουμε διαλέξει σύστημα συντεταγμένων. Οι χρονικές τιμές που αποδίδουμε τότε στα γεγονότα λέγονται "συντεταγμένος χρόνος".
Στην σχετικότητα αυτό που ισχύει είναι ότι τα φυσικά αποτελέσματα είναι αναλλοίωτα κάτω από αλλαγές συντεταγμένων, δηλαδή τα φυσικά αποτελέσματα δεν αλλάζουν όταν αλλάζει αυτός που κάνει την μέτρηση, δηλαδή η φυσική είναι η ίδια για όλους τους παρατηρητές. Φυσικά, μπορεί διαφορετικοί παρατηρητές να μετράνε διαφορετικές τιμές σε κάποια πράγματα, αλλά αυτά που θα μετράνε θα ικανοποιούν τους ίδιους αναλλοίωτους φυσικούς νόμους και η φυσική εικόνα του ενός παρατηρητή θα μετασχηματίζεται ακριβώς στην φυσική εικόνα του άλλου παρατηρητή όταν κάνει κανείς τον μετασχηματισμό από το ένα σύστημα στο άλλο.
Ναι αλλά ο χρόνος που μετρά κάθε παρατηρητής είναι διαφορετικός για συγκεκριμένα γεγονότα.
Αν πάρουμε για παράδειγμα το παράδοξο των διδύμων, βλέπουμε ότι για 2 συγκεκριμένα γεγονότα (αναχώρηση και άφιξη) που συμπίπτουν για τους 2 παρατηρητές, η ενδιάμεση χρονική εξέλιξη είναι διαφορετική για τον καθένα ανάλογα με την ταχύτητα του. Ο ένας γερνάει πιο γρήγορα από τον άλλο.
Άρα ο χρόνος για την σχετικότητα είναι φυσικό μέγεθος από την στιγμή που οι ίδιοι οι παρατηρητές δεν τον αντιλαμβάνονται απλά διαφορετικά, αλλά λειτουργούν και διαφορετικά σαν σώματα.
Δεν είναι μόνο μέτρηση όπως π.χ. όταν 2 παρατηρητές βλέπουν ένα σώμα Χ μήκους ο ένας Ψ και ο άλλος Ζ ανάλογα με την απόσταση τους από αυτό, είναι πραγματικότητα. Σωστά;
Δεν είμαι σίγουρος τι εννοείς με το "ο χρόνος που μετρά κάθε παρατηρητής είναι διαφορετικός για συγκεκριμένα γεγονότα".
Αν οι δυο δίδυμοι αποφασίσουν να μετρήσουν ο ένας τον χρόνο που περνάει για τον άλλον θα συμφωνήσουν στις μετρήσεις που θα πάρουν, αφού αυτό που θα μετρήσει ο κάθε ένας θα είναι το αναλλοίωτο χωροχρονικό μήκος της τροχιάς του καθενός. Θα συμφωνήσουν δηλαδή ότι οι δύο τροχιές στον χωροχρόνο έχουν διαφορετικό μήκος. Το αρχικό και το τελικό γεγονός μπορεί να είναι το ίδιο για τις δύο τροχιές, αλλά το μήκος της κάθε τροχιάς που είναι η χρονική διάρκεια της τροχιάς μπορεί να είναι διαφορετικό, όπως ακριβώς και το μήκος της διαδρομής που συνδέει δύο σημεία στον χώρο μπορεί να είναι διαφορετικό ανάλογα με την διαδρομή που ακολουθείς. Και αυτό είναι που έχει φυσικό νόημα, το χωροχρονικό μήκος $$\reverse\opaque\Delta s$$ (Δs) της διαδρομής, και το νόημά του είναι ότι συνιστά τον ιδιόχρονο του κάθε παρατηρητή (τον χρόνο που δείχνει το ρολόι στο χέρι του). Τα δύο γεγονότα, το αρχικό και το τελικό, δεν συνδέονται με κάποια χρονική διάρκεια a priori όπως συμβαίνει στην Νευτώνεια φυσική.
Είναι όπως και με ένα αυτοκίνητο. Για να δεις σε τι κατάσταση είναι δεν σε ενδιαφέρει σε ποιες πόλεις έχει πάει, αλλά πόσα χιλιόμετρα έχει διανύσει.
Ναι αυτό εννοούσα.
Βέβαια αυτό προϋποθέτει ότι ο χωρόχρονος είναι κάτι που έχει φυσική υπόσταση και όχι ένας φανταστικός/μαθηματικός κόσμος.
Πράγμα που σημαίνει ότι θα έπρεπε να μπορούμε να αλληλεπιδρούμε με τον χωρόχρονο με κάποιο τρόπο και κανονικά ότι θα μπορούσαμε κινούμαστε και σε αυτόν ελεύθερα προς όποια "κατεύθυνση" θέλουμε.
Σωστά;
Στο πλαίσιο της ειδικής σχετικότητας, ο χωροχρόνος είναι μη δυναμική ποσότητα. Αυτό που είναι στην ευχέρεια του κάθε παρατηρητή είναι το να "επιλέξει" την χωροχρονική διαδρομή, την κοσμική τροχιά, που θα ακολουθήσει (με κάποιους περιορισμούς, για παράδειγμα οποιοδήποτε από τα γνωστά μας σωματίδια θα πρέπει να κινείται πάντα σε χρονοειδείς τροχιές, δηλαδή με ταχύτητα μικρότερη από αυτή του φωτός, ενώ ένα σωματίδιο χωρίς μάζα θα πρέπει να κινείται πάντα σε μία φωτοειδή τροχιά με την ταχύτητα του φωτός - μπορεί από την άλλη να υπάρχουν και πεδία που να κινούνται πάντα με ταχύτητα μεγαλύτερη από αυτή του φωτός, βλέπε την συζήτηση εδώ).
Στην γενική σχετικότητα αλλάζουν κάπως τα πράγματα. Ο χωροχρόνος γίνεται δυναμική ποσότητα και το πως κινείται η ύλη ή το πως είναι κατανεμημένη η ύλη και η ενέργεια επηρεάζουν τον χωροχρόνο. Και πάλι όμως ισχύουν τα ίδια πράγματα σε σχέση με την κίνηση και τις "ελευθερίες" που έχουν τα σωματίδια στην επιλογή της κοσμικής τροχιάς τους.
Ωραίο άρθρο συγχαρητήρια, καιρό είχες να γράψεις κάτι αξιόλογο, και για μάς τους κοινούς θνητούς, οχι οτι το αντιλήφθηκα στην ολότητά του, τις εξισώσεις τις προσπέρασα. Για τους Θεοδωσίου και Δανέζη, ισχύει οτι και για τους περισσότερους επιστήμονες και καθηγητές, συμβιβασμένοι και καπελωμένοι απο το πολιτικοθρησκευτικό σύστημα. Παρ΄όλο που ξεκίνησαν ελπιδοφόρα, κάπου χάθηκε το μέτρο, μια σύγκριση με την σειρά COSMOS του Carl Sagan που έβλεπα μικρός, είναι αποκαλυπτική της μικρότητάς τους.
Εύχομαι χρόνια πολλά, καλή χρονιά, με υγεία, και οτι καλύτερο στην ζωή σου.
Αυτοί οι περιορισμοί που αναφέρεις από που προκύπτουν;
Επίσης στην άλλη κουβέντα που με παραπέμπεις αναφέρεις για το παράδοξο των διδύμων ότι βασίζεται σε κακές παραδοχές και εφαρμογή της σχετικότητας. Θεωρείς ότι είναι λάθος, δεν υφίσταται ή κατάλαβα κάτι λάθος;
Οι περιορισμοί προκύπτουν από το ότι ο τρόπος που μετρώνται οι αποστάσεις στον χωροχρόνο έχει Lorentzian χαρακτήρα και όχι Ευκλείδειο, δηλαδή για να βρεις ένα χωροχρονικό μήκος προσθέτεις τα τετράγωνα των χωρικών αποστάσεων (όπως στο Πυθαγόρειο θεώρημα) αλλά αφαιρείς το τετράγωνο της χρονικής "απόστασης". Και αυτό προκύπτει ουσιαστικά από τις ιδιότητες του ηλεκτρομαγνητισμού με τις οποίες προσπάθησε να είναι συνεπής η σχετικότητα.
Όταν λέμε "παράδοξο των διδύμων", εννοούμε μια σειρά από συλλογισμούς που οδηγούν στο παράδοξο αποτέλεσμα ο καθένας δίδυμος να βλέπει τον άλλον δίδυμο να γερνάει πιο αργά και άρα ο καθένας κατά την συνάντησή τους θα είναι πιο γέρος από τον άλλον. Όπως το περιγράφει και η wikipedia στην εισαγωγή,
"In physics, the twin paradox is a thought experiment in special relativity involving identical twins, one of whom makes a journey into space in a high-speed rocket and returns home to find that the twin who remained on Earth has aged more. This result appears puzzling because each twin sees the other twin as traveling, and so, according to a naive application of time dilation, each should paradoxically find the other to have aged more slowly."
Το παράδοξο αυτό λοιπόν δεν υφίσταται. Δηλαδή ο δίδυμος που θα κάνει το ταξίδι θα ακολουθήσει μια χωροχρονική διαδρομή με μικρότερο χωροχρονικό μήκος, δηλαδή μικρότερου ιδιόχρονου, και άρα αυτός θα είναι κατά την επιστροφή ο νεότρος από τους δύο. Το παράδοξο του να μην ξέρεις τελικά ποιος είναι πιο νέος προκύπτει μόνο όταν προσπαθήσει κανείς να εφαρμόσει αφελώς και εσφαλμένα την σχετικότητα.
Ωραίο θέμα και καλογραμμένο άρθρο. Ανυπομονώ για τη συνέχεια. Καλή χρονιά.
@Vagelford
Ευχαριστώ για το μήνυμα. Εξαιρετικά ενδιαφέρον το πως χρησιμοποιείται ο χρόνος στην φυσική. Έχω βέβαια την εντύπωση πως η κοινή γνώμη έχει σε μεγάλο βαθμό άγνοια (μερικώς κατά την άποψη μου υπ ευθύνη των ΜΜΕ που αποτυγχάνουν παταγωδώς στην μετάδοση επιστημονικών ειδήσεων).
@Ανώνυμος
Δίκαιο έχεις στο ότι ίσως σε κάποιο βαθμό οι επιστήμονες πάσχουν από το σφάλμα της πραγμάτωσης. Και είναι επικίνδυνο όταν δεν το συνειδητοποιούν αυτό. Χαίρομαι που σου αρέσει το blog μου και ναι με ενδιαφέρει η συν-ολοκλήρωση και γενικά οι μη στάσιμες χρονοσειρές. Πως και με ρωτάς;
Epanechnikov, δυστυχώς όπως θα είδες δεν είναι μόνο τα ΜΜΕ που δεν μπορούν να ενημερώσουν τον κόσμο για τις επιστημονικές εξελίξεις, αλλά σίγουρα έχουν μεγάλη ευθύνη.
Σχετικό με το άρθρο βίντεο. Ο Ηawking για πραγματικό και φαντασιακό χρόνo:
http://youtu.be/HKQQAv5svkk?t=13m17s
Epan, εδώ αυτό που λέει ο Hawking δεν είναι "φαντασιακός" χρόνος αλλά φανταστικός χρόνος με την μαθηματική έννοια, δηλαδή χρόνος που ορίζεται ως $$\reverse\opaque \tau = i t $$ και είναι ένας φανταστικός αριθμός (οι μιγαδικοί αριθμοί έχουν πραγματικό και φανταστικό μέρος, $$\reverse\opaque z = a + i b $$, όπου η φανταστική μονάδα είναι η ρίζα του -1).
Αυτό το τρικ είναι παλιό. Χρησιμοποιήθηκε αρχικά για να δώσει ευκλείδειο μέτρο στην μετρική της ειδικής σχετικότητας, αφού άμα πάρεις φανταστικό τον χρόνο, το τετράγωνό του είναι αρνητικό. Χρησιμοποιείται επίσης στην κβαντική θεωρία πεδίου. Δεν είχα δει ότι έχει κάποια εφαρμογή στην κοσμολογία.
Το συγκεκριμένο trick δεν το γνώριζα μιας και δεν έχω ασχοληθεί επιστημονικά με την ειδική σχετικότητα (το στενότερο γνωστικό αντικείμενο στη φυσική με το οποίο έχω ασχοληθεί είναι μάλλον τα δυναμικά συστήματα και η φασματική ανάλυση). Φανταστικός λοιπόν χρόνος, αν κατάλαβα καλά, είναι το imaginary part κάποιου μιγαδικού map του χρόνου.
Το σχετικό με την συζήτηση μας είναι το explicatum "φανταστικός χρόνος" είναι ένα μαθηματικό κατασκεύασμα που αναφέρεται σε διαφορετικό διαφορετικό explicandum από ότι αναφέρεται το expicatum ordinary χρόνος (αυτός που μετράμε με τα ρολόγια μας). Η σύγχυση των δύο μπορεί να οδηγήσει σε εξόχως άσχετα δανέζιου τύπου new-age συμπεράσματα.
Μου άρεσε και το τελευταίο σου άρθρο για τον χρόνο. Το ερώτημα μου είναι πως είναι δυνατόν καθηγητές φυσικής να αγνοούν ή να παρερμηνεύουν πράγματα που φαίνονται πολύ βασικά. Δεν μιλάμε για λεπτές έννοιες αλλά για τα θεμελιώδη.
Μερικά πραγματάκια σχετικά με τον φανταστικό χρόνο μπορείς να δεις στο άρθρο της wikipedia για το Wick rotation. Στην ουσία δεν θεωρείς κάποιο μιγαδικό map, αλλά κάνεις μια στροφή από τον πραγματικό άξονα για τον χρόνο στον φανταστικό άξονα.
Σχετικά με την σύγκριση και τη σύγχυση ανάμεσα στα explicatum και explicandum των "φανταστικός χρόνος" και "συνήθης χρόνος", είναι έτσι όπως τα λες και το φαινόμενο είναι πολύ συχνό.
Και εμένα μου είναι αδιανόητο το πως γίνεται να έχει παρερμηνεύσει κανείς τόσο πολύ τόσο βασικές έννοιες. Είναι πραγματικά απορίας άξιο και κρίμα. Έχω όμως μία θεωρία...
Αν έχεις σχόλια για το άλλο άρθρο, θα χαρώ να τα δω.
Καλησπέρα
Έχεις υπόψη σου την έννοια του αφηρημένου χρόνου και της αφηρημένης εργασίας στον Μαρξ? Αν ναι, πως θα την σχολίαζες? Οι κομμουνάροι όταν εξεγέρθηκαν, έλεγε ο Μπένγιαμιν, ότι έσπαγαν τα ρολόγια. Το ρολόι είναι αυτό που υποτάσσει τις ποιότητες (της εργασιακής διαδικασίας πχ) στην μετρησιμότητα.
Η έννοια του αφηρημένου χρόνου, δηλαδή η ανάγκη να "φυσικοποιούμε" κοινωνικές μορφές (σε αντίθεση με το βάρος πχ) είναι κάτι που συναντάμε παντού σήμερα: "πόσες ώρες διάβασες", "διάβασα 5 ώρες". "Πόσο μακριά είναι?", "ένα τσιγάρο δρόμος".
Σόρρυ για την αρχαϊκή διατύπωση του σχολίου
Χάρης
Γεια σου JKL.
Δυστυχώς δεν τον ξέρω τον αφηρημένο χρόνο του Μάρξ.
Πάντως ο χρόνος στη φυσική είναι μία μετρήσιμη φυσική ποσότητα (με την εντελώς χαλαρή έννοια του όρου "φυσική ποσότητα" για να μην μπω σε οντολογικά θέματα σχετικά με το "τι είναι χρόνος") και όχι κάποια κοινωνική μορφή. Δεν είναι κοινωνική μορφή ο χρόνος για το μιόνιο για παράδειγμα το οποίο έχει χρόνο ζωής περίπου 2.2μs στο σύστημα ηρεμίας του από τη στιγμή που παράγεται μέχρι να διασπαστεί πχ. σε ένα ηλεκτρόνιο και τα κατάλληλα νετρίνα. Το μιόνιο δεν καταλαβαίνει ούτε από κοινωνίες ούτε από εργασία.
(Και φυσικά δεν έχει κανένα DNA για να το οδηγεί σε πλάνες των αισθήσεων, όπως αρέσει σε κάποιον να λέει ότι είναι ο χρόνος)
Η όλη συζήτηση στο συγκεκριμένο post είναι για τον χρόνο στη φυσική και όχι για τις πιθανές κοινωνικές, οικονομικές, ιστορικές ή πολιτικές διαστάσεις του.
Γεια σου Vagelford!
Αν έχεις την καλοσύνη, πες μου αν το έχω πιάσει σωστά:
0) Ο χρόνος έχει νόημα (υπάρχει) μόνο όταν υπάρχουν γεγονότα.
1) Γεγονός (όπως το αντιλαμβάνομαι εγώ), σημαίνει αλλαγή (μεταβολή κατάστασης).
2) Για κάποιον που ζει μέσα σε ένα σύστημα Α, όπου συμβαίνουν γεγονότα, ο χρόνος (που αντιλαμβάνεται) ρέει πάντα "κανονικά". Επειδή πολύ απλά, αυτός ο κάποιος αποκτά συνείδηση, ακριβώς επειδή υπάρχουν αυτά τα διαδοχικά γεγονότα (τα τουρλοπηδήματα των στοιχειωδών σωματίδιων που προσδίνουν "λειτουργία" στον εγκέφαλό του και τού επιτρέπουν να είναι "παρατηρητής").
3) Κάποιος άλλος έξω από το σύστημα Α, με βάση την ροή τού χρόνου στο δικό του σύστημα Β, μπορεί να "κρίνει" ότι η ροή των γεγονότων (άρα και ο χρόνος) στο σύστημα Α "προχωράει ανώμαλα": με διακοπές, "επιταχύνσεις", "επιβραδύνσεις" κ.λπ..
4) Φυσικά, και ο παρατηρητής στο σύστημα Α, αν παρακολουθεί το Β θα βγάλει το συμπέρασμα ότι εκεί ο χρόνος κυλάει ανώμαλα.
5) Βέβαια. υπάρχει το θέμα πώς θα φτάνει (τι αλλοιώσεις θα παθαίνει) η πληροφορία καθώς θα πηγαίνει από το ένα σύστημα στο άλλο. Άρα το παραπάνω πείραμα είναι κυρίως νοητό.
Σωστά ως εδώ;
6) Άρα αυτό που εννοεί ο Δ. στο 1ο βίντεο, είναι ότι αν υπήρχε ένας εξωτερικός παρατηρητής τού Σύμπαντός μας, θα το έβλεπε να (απο)καμπυλώνεται και ταυτόχρονα να αλλάζει ο χρόνος (ο ρυθμός των διαδοχικών γεγονότων) μέσα του.
(ΑΝ φυσικά ο εξ. παρατηρητής ζούσε σε ένα σύστημα με "σταθερή" (απαρπάλλαχτη) καμπύλωση και όλα τα άλλα.)
7) Αυτό όμως δεν σημαίνει ότι για όσους ζουν μέσα στο Σύμπαν μας δεν αντιλαμβάνονται μία "πραγματική συσσώρευση" χρόνου (ακριβέστερα: γεγονότων) από την απαρχή τής δημιουργίας του.
Οπότε, για αυτό τον κράζεις, σωστά;
8) Αν ναι, ωραία. Τίθεται λοιπόν το ερώτημα:
Δεν μπορούμε όλοι μαζί, όσοι ζούμε σε διάφορα συστήματα, να καθορίσουμε μία απόλυτη μονάδα χρόνου; (Ή σωστότερα: μία "παγκόσμια" μονάδα "γεγονότος";)
9) Αυτή η απόλυτη μονάδα γεγονότος, θα έπρεπε να είναι και στοιχειώδης μονάδα; Δηλαδή η μικρότερη που μπορεί να υπάρξει;
Υπάρχει κάτι σαν "κβάντο γεγονότος";
10) Θα μπορούσε να είναι το πόσοι πυρήνες σπάνε από μία ραδιενεργό ουσία; Από όσο ξέρω είναι το μόνο τυχαίο γεγονός που αναγνωρίζει η φυσικά, άρα είναι η μόνη "ανεξάρτητη μεταβλητή" στο Σύμπαν, οπότε σκέφτομαι μήπως όλες και όλα τα άλλα μπορούν και πρέπει αν ορίζονται βάσει αυτής. Μεταξύ άλλων και η ροή (ύπαρξη) χρόνου.
Τα 9 και 10 είναι σπεκουλέισόνς μου και μάλλον ξεφεύγουν από το θέμα, αλλά αν μπορείς να μού πεις αν στέκουν τα 0 έως 8 θα με βοηθήσεις πολύ.
Idom
Γεια σου Idom.
0) Τα γεγονότα δεν υπάρχουν από μόνα τους. Για να έχεις ένα γεγονός πρέπει να έχεις κάποια άλλα στοιχεία τα οποία θα συνιστούν το γεγονός. Για παράδειγμα η σκέδαση δύο σωματιδίων ή το σκάσιμο της κροτίδας που αναφέρω παραπάνω προϋποθέτουν την ύπαρξη των σωματιδίων και της κροτίδας και των θραυσμάτων της. Μπορεί δηλαδή τα γεγονότα να είναι θεμελιώδεις μονάδες όπου μια ακολουθία από αυτά δημιουργεί μια κοσμική γραμμή για ένα σωματίδιο κλπ., αλλά από φυσική άποψη το σωματίδιο είναι αυτό που είναι θεμελιώδες.
Έτσι η ύπαρξή του σωματιδίου μέσα στον τετραδιάστατο χωροχρόνο είναι αυτή που ορίζει την κοσμική του γραμμή (που είναι μια ακολουθία γεγονότων) η οποία με τη σειρά της ορίζει έναν χρόνο, που θα είναι ο χρόνος που μετρά αυτό το σωματίδιο. Η εισαγωγή ενός σωματιδίου (το οποίο πρέπει να έχει μάζα και να μην είναι φωτόνιο) λοιπόν εισάγει την έννοια του χρόνου.
1) Το γεγονός είναι κάτι στιγμιαίο. Δεν έχει διάρκεια. Πάνω σε μια κοσμική γραμμή (αυτή περιγράφει μια εξέλιξη ας πούμε) ένα γεγονός είναι το σύνορο ανάμεσα σε δύο περιοχές της κοσμικής γραμμής που την χωρίζει στα σημεία (γεγονότα) πριν από αυτό και μετά από αυτό κατά μήκος της.
2-5) Θα μπορούσες να το πεις και έτσι, αν και για τα πιο σύνθετα συστήματα, όπως είναι ένας άνθρωπος, η κατάσταση είναι λίγο πιο περίπλοκη. Αυτός ο κάποιος πάντως ορίζει ένα σύστημα. Δεν είναι επισκέπτης απλά. Αυτό που χρησιμοποιώ εγώ ως παράδειγμα είναι το μιόνιο το οποίο έχει χρόνο ζωής περίπου 2.2μs μετά από τα οποία διασπάτε και έτσι ορίζει σαφώς ένα αδιαμφισβήτητο ρολόι.
Δημιουργήθηκε (από την σκέδαση κάποιων άλλων σωματιδίων, γεγονός), πέρασε κάποιος χρόνος (κοσμική γραμμή), διασπάστηκε (σε άλλα σωματίδια, γεγονός). Σαφές.
Αν τώρα το μιόνιο το παρατηρεί κάποιος άλλος ως προς τον οποίο το σωματίδιο κινείτε με μεγάλη ταχύτητα, τότε αυτός δεν θα το δει να ζει για 2.2μs αλλά για περισσότερο, πράγμα που θα τον οδηγήσει στην σκέψη ότι το ρολόι του μιονίου τρέχει πιο αργά. Αυτό το βλέπουμε πρακτικά με τα μιόνια που δημιουργούνται από τις κοσμικές ακτίνες στα ανώτερα στρώματα της ατμόσφαιρας. Αν και τα μιόνια που δημιουργούνται κινούνται με την ταχύτητα του φωτός, μέσα στα 2.2μs δεν θα προλάβαιναν να φτάσουν στο έδαφος. Εμείς όμως τα μετράμε με ανιχνευτές στο έδαφος, πράγμα το οποίο σημαίνει ότι στο σύστημά μας τα μιόνια ζουν περισσότερο.
Ελπίζω για αρχή να σε έχω καλύψει μέχρι εδώ, αν και θα έλεγα ότι μάλλον σωστά το έχεις καταλάβει.
(συνέχεια...)
(...συνέχεια)
6,7) Τώρα, αυτό δεν έχει και πολύ νόημα. Τι σημαίνει ο παρατηρητής έξω από το σύμπαν; Ή για να το πω διαφορετικά, δεν ξέρω τι νόημα να του δώσω. Ο Δανέζης πάντως δεν νομίζω ότι εννοεί αυτό το πράγμα. Αν θέλεις να δεις ακριβώς γιατί "τον κράζω" γενικά, καλύτερα είναι να δεις το Not Even Wrong. Στο συγκεκριμένο πάντως και σχετικά με τον χρόνο γενικά και τον χρόνο στην κοσμολογία ειδικά, αυτό που λες στο 7 είναι υπό μία έννοια η ουσία που διαφεύγει εντελώς από τον Δανέζη.
Δηλαδή, για να το πω διαφορετικά, αν ας πούμε το πρωτόνιο ήταν ασταθές (θεωρητικά δεν είναι ασταθές και άρα δεν διασπάτε ποτέ) και είχε διάρκεια ζωής μερικά δισεκατομμύρια χρόνια, τότε κάποια στιγμή όλη η παρατηρήσιμη ύλη, η ύλη από την οποία αποτελούμαστε και εμείς, θα άρχιζε να διασπάτε όπως ακριβώς μετά από κάποιο χρονικό διάστημα διασπάτε το μιόνιο. Και αυτό οφείλετε στο ότι το κάθε πρωτόνιο θα έφτανε να έχει ζήσει τόσο χρόνο όσο είναι η διάρκεια ζωής του. Θα είχε δηλαδή μετρήσει τόσο ιδιόχρονο όσο είναι η διάρκεια ζωής του. Το επόμενο ερώτημα ενδεχομένως είναι αν αυτό θα γινόταν ταυτόχρονα (με προσοχή λίγο στο τι σημαίνει ταυτόχρονα) για όλα τα πρωτόνια στο σύμπαν. Και η απάντηση είναι περίπου ναι και ο κοσμολογικός χρόνος, η εποχή, που θα συνέβαινε αυτό θα ήταν όταν το σύμπαν θα είχε ηλικία περίπου όσο είναι η διάρκεια ζωής του πρωτονίου. Τώρα, αυτό δεν είναι απόλυτα ακριβές, γιατί άλλη διάρκεια έχει καταγράψει ένα πρωτόνιο που είναι σε ένα άτομο Υδρογόνου μέσα σε ένα νέφος υδρογόνου, άλλη διάρκεια έχει καταγράψει ένα πρωτόνιο που κινείται με σχετικιστικές ταχύτητες, άλλη διάρκεια έχει καταγράψει ένα πρωτόνιο που είναι μέσα σε έναν πιο βαρύ πυρήνα, και σε τελική ανάλυση δεν έχουν δημιουργηθεί όλα τα πρωτόνια μαζί. Αλλά η ουσία είναι ότι η κοσμολογική εποχή της διάσπασης του κάθε πρωτονίου θα ήταν συνεπής με τον ιδιόχρονο που έχει καταγράψει.
(συνέχεια...)
(...συνέχεια)
Και πέρα από αυτό, υπάρχει ένας παγκόσμιος χρόνος που μπορεί να ορισθεί για όλους τους παρατηρητές που βρίσκονται μέσα στο σύμπαν και τον μετράνε όλοι το ίδιο. Αυτός είναι ο χρόνος των παρατηρητών που είναι ακίνητοι μέσα στο σύμπαν ως προς τον χωροχρόνο και αφήνουν τη διαστολή του χωροχρόνου (που την λέμε κοσμική ροή ή ροή Hubble) να τους παρασύρει όπως παρασέρνει η ροή ένα φύλλο στην επιφάνεια ενός ρυακιού. Αν για παράδειγμα φανταστούμε το σύμπαν σαν την επιφάνεια ενός μπαλονιού το οποίο φουσκώνει σιγά σιγά, οι παρατηρητές αυτοί βρίσκονται πάνω σε κάποιες ζωγραφισμένες κουκκίδες οι οποίες βλέπουν η μία την άλλη να απομακρύνετε αλλά καμία δεν κινείται ως προς την επιφάνεια (έχουν πάντα το ίδιο γεωγραφικό μήκος και πλάτος).
Κοσμολογικά το ανάλογο αυτής της επιφάνειας είναι ο τρισδιάστατος χώρος του σύμπαντος και η αλλαγή της κλίμακας του μήκους πάνω σε αυτή την επιφάνεια είναι η διαστολή του σύμπαντος, ενώ ο χρόνος που μετράνε αυτοί οι παρατηρητές θα μπορούσε να συνδεθεί με την ακτίνα του μπαλονιού. Όταν η ακτίνα του μπαλονιού είναι κοντά στο μηδέν, τότε έχουμε την αρχή και καθώς μεγαλώνει η ακτίνα μετράμε χρόνο. Και όλες οι κουκκίδες στην επιφάνεια του μπαλονιού μετράνε τον ίδιο χρόνο. Στο πραγματικό σύμπαν λοιπόν οι παρατηρητές που αντιστοιχούν στις κουκκίδες του μπαλονιού είναι με καλή ακρίβεια οι γαλαξίες. Και όσοι παρατηρητές βρίσκονται μέσα στους γαλαξίες μετράνε αυτόν ακριβώς τον κοσμολογικό χρόνο (με κάποιες διορθώσεις λόγω εσωτερικών ενδεχομένως διαδικασιών, όπως οι κινήσεις που μπορεί να κάνει ο καθένας μέσα στο γαλαξία του ή οι διορθώσεις από τοπικά βαρυτικά πεδία, κλπ.) ο οποίος είναι στην πραγματικότητα ο ιδιόχρονος του συστήματος στο οποίο βρίσκεται ο κάθε γαλαξίας. Αυτόν τον χρόνο (με τις διορθώσεις που αναφέρω παραπάνω) θα μετρά και ένα ασταθές σωματίδιο που μετρά τον χρόνο μέχρι να διασπαστεί και αυτός ο χρόνος έχει την ίδια ροή σε όλες τις εποχές της εξέλιξης του σύμπαντος και αυτός είναι ο χρόνος για τον οποίον μιλάνε οι κοσμολόγοι (και νομίζω ότι αυτό απαντά σε ένα κομμάτι του ερωτήματος 8).
Τώρα, σχετικά με το 9 και το θέμα του κβάντου του χρόνου, αυτό είναι ένα άλλο θέμα που δεν μπορεί να απαντηθεί στα πλαίσια της σχετικότητας, αλλά δεν χρειάζεται κιόλας να απαντηθεί στα πλαίσια της παραπάνω κουβέντας.
Για το 10, μερικώς πρέπει να σε έχω καλύψει με όσα είπα παραπάνω για τα ασταθή σωματίδια και το πως η διάρκεια ζωής τους μετρά τον χρόνο. Δηλαδή ουσιαστικά μπορείς να χρησιμοποιήσεις και τις ραδιενεργές διασπάσεις ως ρολόι αντί για την διάρκεια ζωής ενός ασταθούς σωματιδίου, αν και μπορεί να υπάρχουν κάποιες περιπλοκές επειδή και πάλι μιλάμε για πυρήνες που είναι πιο περίπλοκα συστήματα από ένα απλό σωματίδιο.
Το πλάνο είναι να υπάρξει ένα ανεξάρτητο post στη συνέχεια στο οποίο να αναλύονται τα όσα αναφέρω περιληπτικά παραπάνω για τον χρόνο στην κοσμολογία.
Ελπίζω να απάντησα σε γενικές γραμμές στα ερωτήματά σου Idom.
Να είσαι καλά.
ΧΑΙΡΕΤΕ.
ΕΑΝ Η ΤΑΧΥΤΗΤΑ ΜΕΤΑΔΟΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ ΔΕΝ ΗΤΑΝ ΠΕΡΙΟΡΙΣΜΕΝΗ ΑΠΟ ΤΟ C=300.000Km/sec ΑΛΛΑ ΗΤΑΝ ΑΠΕΡΙΟΡΙΣΤΗ - ΑΠΕΙΡΗ ΤΟΤΕ ΘΑ ΜΠΟΡΟΥΣΑΜΕ ΝΑ ΕΧΟΥΜΕ ΕΝΑ ΧΩΡΟ ΧΩΡΙΣ ΧΡΟΝΟ?
Γεια σου Ανδρέα.
Η περίπτωση όπου η ταχύτητα του φωτός είναι άπειρη είναι η Νευτώνεια περίπτωση, όπου δηλαδή έχεις έναν απόλυτο χρόνο για όλους τους παρατηρητές.
Ευχαριστώ Vagelford για την παράθεση. Κατάλαβα τι εννοείς διαβάζοντας το αθρο περί Wick rotation.
Ποια είναι η θεωρία σου στην οποία αναφέρεσαι;
Το πρόβλημα όμως είναι πως για τον κάθε δίδυμο, ο άλλος ταξιδεύει. Το πρόβλημα πιθανώς έχει να κάνει με τις επιταχύνσεις.
Δημοσίευση σχολίου