Ανέβηκε σήμερα στο arXiv η εργασία με τίτλο, Kinematical and chemical vertical structure of the Galactic thick disk II. A lack of dark matter in the solar neighborhood (accepted in Astrophysical Journal), η οποία διερευνά την κατανομή της σκοτεινής ύλης στην γειτονιά του Ηλιακού μας Συστήματος. Συγκεκριμένα το abstract της εργασίας λέει,
We estimated the dynamical surface mass density $$\reverse\opaque\Sigma$$ at the solar position between Z=1.5 and 4 kpc from the Galactic plane, as inferred from the kinematics of thick disk stars. The formulation is exact within the limit of validity of a few basic assumptions. The resulting trend of $$\reverse\opaque\Sigma(Z)$$ matches the expectations of visible mass alone, and no dark component is required to account for the observations. We extrapolate a dark matter (DM) density in the solar neighborhood of $$\reverse\opaque 0\pm 1 mM_{\odot} pc^{-3}$$, and all the current models of a spherical DM halo are excluded at a confidence level higher than $$\reverse\opaque 4\sigma$$. A detailed analysis reveals that a small amount of DM is allowed in the volume under study by the change of some input parameter or hypothesis, but not enough to match the expectations of the models, except under an exotic combination of non-standard assumptions. Identical results are obtained when repeating the calculation with kinematical measurements available in the literature. We demonstrate that a DM halo would be detected by our method, and therefore the results have no straightforward interpretation. Only the presence of a highly prolate (flattening q>2) DM halo can be reconciled with the observations, but this is highly unlikely in ΛCDM models. The results challenge the current understanding of the spatial distribution and nature of the Galactic DM. In particular, our results may indicate that any direct DM detection experiment is doomed to fail, if the local density of the target particles is negligible.
Με λίγα λόγια δηλαδή, οι C. Moni Bidin, G. Carraro, R. A. Mendez και R. Smith λένε ότι από παρατηρήσεις των ταχυτήτων άστρων που βρίσκονται στη γειτονιά του Ηλιακού μας συστήματος, έκαναν ένα δυναμικό υπολογισμό της πυκνότητας της μάζας στον δίσκο του Γαλαξία μας στην θέση του Ήλιου (όπως αυτός εκφράζεται από την επιφανειακή πυκνότητα της μάζας ως συνάρτηση του ύψους z, που δίνεται από το ολοκλήρωμα $$\reverse\opaque \Sigma(Z)=\int_{-Z}^Z\rho(z)dz$$) και βρήκαν ότι η δυναμική υποδεικνύει ότι η μάζα που περιέχεται σ'αυτή την περιοχή είναι σχεδόν τόση όση και η μάζα που υπολογίζεται από την φωτεινή ύλη, ενώ το περιεχόμενο σε σκοτεινή ύλη περιορίζεται σε $$\reverse\opaque 0\pm 1 mM_{\odot} pc^{-3}$$, δηλαδή λιγότερο από 1 χιλιοστό της ηλιακής μάζας ανά κυβικό parsec.
Τι σημαίνουν όμως όλα αυτά;
Ας αρχίσουμε με τον δυναμικό υπολογισμό της μάζας.
Ένας γαλαξίας, αποτελεί μια μεγάλη συγκέντρωση άστρων και αερίου, τα οποία όλα μαζί κινούνται υπό την επίδραση του βαρυτικού πεδίου που παράγουν. Ουσιαστικά το όλο σύστημα αποτελεί αυτό που λέμε, ένα πρόβλημα Ν σωμάτων, όπου το κάθε άστρο είναι ένα από τα Ν σώματα. Επειδή ακριβώς, ο αριθμός Ν αυτών των σωμάτων είναι πολύ μεγάλος, το υλικό του γαλαξία μπορεί να μοντελοποιηθεί ως ένα ρευστό σκόνης με ιδιοβαρύτητα, δηλαδή ένα ρευστό που ουσιαστικά δεν έχει πίεση και οδηγείται από την βαρύτητα του υλικού που το αποτελεί.
Γενικά, η εξίσωση κίνησης για ένα ρευστό με ιδιοβαρύτητα έχει την μορφή,
$$\reverse\opaque\frac{\partial(\rho U_i)}{\partial t}+\vec{\nabla}\cdot(\rho U_i \vec{U})=-(\vec{\nabla}P)_i-\rho(\vec{\nabla}\Phi)_i,$$
όπου ρ είναι η πυκνότητα της μάζας, U είναι το πεδίο ταχυτήτων του ρευστού και Φ είναι το βαρυτικό δυναμικό. Η εξίσωση αυτή ουσιαστικά αποτελεί μια γενίκευση του 2ου νόμου του Νεύτωνα
$$\reverse\opaque \rho a_i=f_i,$$
για την περίπτωση όμως ενός ρευστού όπου έχουμε κατανομές μάζας και άρα πυκνότητες. Στην περίπτωση που το ρευστό είναι σκόνη, τότε δεν υπάρχει πίεση και άρα ο όρος $$\reverse\opaque \vec{\nabla}P$$ δεν υπάρχει στην εξίσωση. Για να μπορέσουμε να περιγράψουμε την κίνηση του ρευστού, χρειαζόμαστε ακόμα μία εξίσωση που να μας δίνει το βαρυτικό δυναμικό και αυτή είναι η εξίσωση του πεδίου βαρύτητας,
$$\reverse\opaque \vec{\nabla}\cdot\vec{g}=-\nabla^2\Phi=-4\pi G\rho,$$
όπου $$\reverse\opaque \vec{g}=-\vec{\nabla}\Phi$$. Το πεδίο βαρύτητας γενικά δεν είναι απαραίτητο να δημιουργείται μόνο από την κατανομή της ύλης της οποίας την κίνηση μελετάμε. Έτσι η πυκνότητα της μάζας ρ στην τελευταία εξίσωση, είναι η πυκνότητα όλης της βαρυτικής μάζας που δημιουργεί πεδίο. Έτσι η τελευταία εξίσωση μπορεί ουσιαστικά να χρησιμοποιηθεί για να "ανιχνεύσει" κανείς την ύλη που υπάρχει και προκαλεί βαρυτικό πεδίο, από τον τρόπο κίνησης ενός ρευστού του οποίου η κίνηση περιγράφεται από την πρώτη εξίσωση.
Επιστρέφοντας λοιπόν στο πρόβλημα του γαλαξία, η κίνηση των άστρων μπορεί να περιγραφεί από την πρώτη εξίσωση (χωρίς την πίεση) δεδομένου του βαρυτικού πεδίου που υπάρχει στον γαλαξία. Το βαρυτικό πεδίο όμως δεν μπορεί να το δει κανείς παρά μόνο από το αποτέλεσμα του στην κίνηση των σωμάτων, οπότε αυτό που γίνεται είναι η αντίστροφη διαδικασία, δηλαδή από την κίνηση των άστρων εκτιμά κανείς το βαρυτικό πεδίο και άρα την κατανομή της μάζας σε έναν γαλαξία. Δηλαδή, από την πρώτη εξίσωση και τις παρατηρούμενες κινήσεις, γίνεται η εκτίμηση του βαρυτικού πεδίου g το οποίο μετά το χρησιμοποιούμε στην εξίσωση πεδίου του Νεύτωνα (την δεύτερη εξίσωση) για να υπολογίσουμε την κατανομή της μάζας.
Με την βοήθεια αυτού του αλγόριθμου και από την μέτρηση του προφίλ των ταχυτήτων των άστρων σε διάφορους γαλαξίες, διαπιστώσαμε ότι η παρατηρούμενη ύλη (η φωτεινή ύλη αποτελούμενη από άστρα και νέφη) ήταν λιγότερη από την πυκνότητα της ύλης που υπολογίζαμε δυναμικά, αφού οι καμπύλες περιστροφής των γαλαξιών (οι καμπύλες που δείχνουν την γωνιακή ταχύτητα ως συνάρτηση της απόστασης), αντί να πέφτουν με την απόσταση από το κέντρο του γαλαξία, παρέμεναν σταθερές. Αυτός ήταν ένας από τους λόγους που εισάγαμε την υπόθεση της σκοτεινής ύλης.
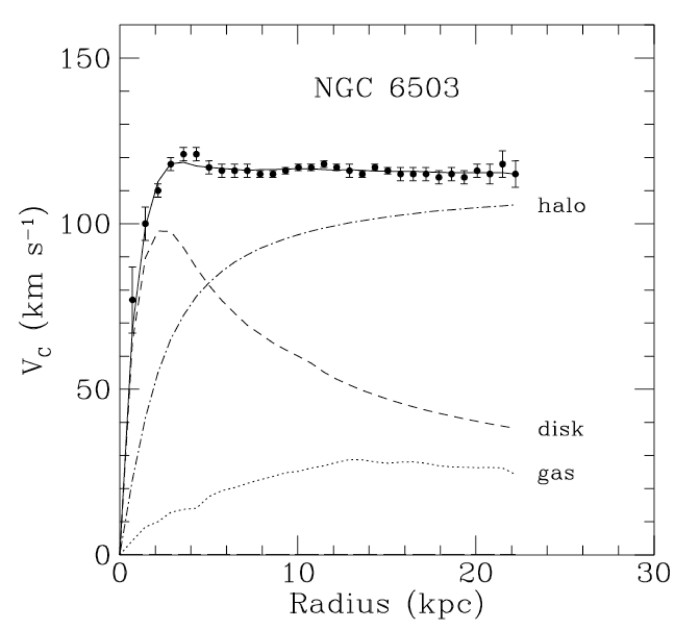
Ένας πρόχειρος υπολογισμός μπορεί να μας δείξει ότι για να έχει κανείς επίπεδη κατανομή ταχυτήτων, η πυκνότητα θα πρέπει να πηγαίνει σαν $$\reverse\opaque \rho\propto\frac{1}{r^2}$$ για σφαιρική κατανομή μάζας.
Γενικά για τους σπειροειδείς γαλαξίες από τις παρατηρήσεις και τους σχετικούς δυναμικούς υπολογισμούς έχουμε ότι η κατανομή της μάζας μπορεί να περιγραφεί από έναν δίσκο με εκθετικό προφίλ μάζας (φωτεινή ύλη) και μια σφαιρική κατανομή μάζας (σκοτεινή ύλη) με μια κεντρική περιοχή συγκεκριμένων διαστάσεων και σταθερής πυκνότητας, πέρα από την οποία η πυκνότητα μειώνεται (The Intriguing Distribution of Dark Matter in Galaxies, Lect.Notes Phys. 616 (2003) 66-77). Συγκεκριμένα ο νόμος της κατανομής της σκοτεινής ύλης μπορεί να δοθεί στην μορφή,
$$\reverse\opaque \rho(r)=\frac{\rho_0 r_0^3}{(r_0+r)(r_0^2+r^2)},$$
όπου οι παράμετροι ρ_0 και r_0 έχουν να κάνουν με την πυκνότητα της σκοτεινής ύλης στην κεντρική περιοχή και τις διαστάσεις αυτής της περιοχής.
Μια παρόμοια μοντελοποίηση της κατανομής της σκοτεινής ύλης για τον Γαλαξία μας μπορεί να βρει κανείς εδώ, Distribution of Dark Matter in the Milky Way, όπου η κατανομή έχει την μορφή,
$$\reverse\opaque \rho(r)=\rho_0\left(\frac{a^2+r_0^2}{a^2+r^2}\right),$$
όπου ρ_0 είναι η "εικαζόμενη" πυκνότητα της σκοτεινής ύλης στην περιοχή του Ήλιου, r_0 είναι η απόσταση του Ήλιου από το κέντρο του Γαλαξία και α είναι το μέγεθος της κεντρικής περιοχής της κατανομής της σκοτεινής ύλης. Γενικά όμως υπάρχουν αρκετά μοντέλα σφαιρικών κατανομών σκοτεινής ύλης (που όμως είναι λίγο-πολύ σ'αυτή τη λογική).
Ας επιστρέψουμε λοιπόν στην συγκεκριμένη εργασία.
Στην συγκεκριμένη εργασία λοιπόν, οι Bidini et al. αυτό που έκαναν ήταν να εφαρμόσουν την παραπάνω ανάλυση, χρησιμοποιώντας ως "ανιχνευτές" του βαρυτικού πεδίου την κίνηση ~400 άστρων (ερυθρών γιγάντων) σε ύψος από το επίπεδο του δίσκου από 1.5 kpc μέχρι 4 kpc από την μεριά του νότιου γαλαξιακού πόλου και στην απόσταση από το γαλαξιακό κέντρο που βρίσκεται και ο Ήλιος. Επειδή όμως τα παρατηρησιακά δεδομένα που είχαν στη διάθεσή τους, δεν περιελάμβαναν όλες τις πληροφορίες που χρειάζονταν σχετικά με τις διασπορές των ταχυτήτων, τις λεπτομέρειες της ακτινικής μεταβολής του προφίλ κλπ., εκτός από τα δεδομένα, η ανάλυσή τους περιέχει και αρκετές υποθέσεις. Το συμπέρασμα που έβγαλαν λοιπόν είναι ότι η επιφανειακή πυκνότητα της μάζας (όπως προκύπτει από την ολοκλήρωση στο z της εξίσωσης πεδίου) ως συνάρτηση του Ζ για την περιοχή του Ήλιου, συμπίπτει με αυτή που θα έπαιρνε κανείς αν υπολόγιζε μόνο την ορατή ύλη (άστρα και νέφη).
Δηλαδή, στην περιοχή που κοιτάμε, η εξίσωση πεδίου μας δίνει πυκνότητα σκοτεινής ύλης σχεδόν μηδέν.
Αυτό το αποτέλεσμα δεν αποκλείει την ύπαρξη σκοτεινής ύλης στο Γαλαξία γενικά. Αυτό που λέει αυτό το αποτέλεσμα είναι ότι με δεδομένες τις υποθέσεις που έχουν γίνει για τις διασπορές των ταχυτήτων (μία από τις οποίες είναι για παράδειγμα και το ότι η κατανομή των γωνιακών ταχυτήτων είναι επίπεδη), την κατανομή της σκοτεινής και της φωτεινής ύλης κλπ., το μοντέλο της σφαιρικής κατανομής της σκοτεινής ύλης και οι μέχρι τώρα υποθέσεις μας για την τοπική πυκνότητα σκοτεινής ύλης φαίνεται να αποκλείονται από την συγκεκριμένη ανάλυση. Οπότε, το θέμα ανάγεται στην ποιότητα των παρατηρήσεων και την ορθότητα των υποθέσεων που έχουν γίνει. Στην εργασία υπάρχει αρκετή επιχειρηματολογία και μια σειρά από ελέγχους που έχουν ως στόχο να δείξουν ότι οι υποθέσεις τους είναι αρκετά στέρεες. Οι λεπτομέρειες αυτής της ανάλυσης ξεφεύγει δυστυχώς από το δικό μου πεδίο.
Ένα από τα θέματα που ελέγχουν πάντως, είναι και εναλλακτικά μοντέλα για την κατανομή της σκοτεινής ύλης και αυτό που βγάζουν είναι ότι μια κατανομή σκοτεινής ύλης με την μορφή σφαιροειδούς με επιμήκυνση κατά τον άξονα των πόλων, θα συμφωνούσε με τα αποτελέσματά τους και με τις παρατηρούμενες καμπύλες περιστροφής, αλλά και πάλι η πυκνότητα της σκοτεινής ύλης στην περιοχή μας θα πρέπει να είναι πολύ μικρότερη από όσο εκτιμάται σήμερα (γενικά οι εκτιμήσεις μιλάνε για 5-13 φορές περισσότερη σκοτεινή ύλη από όσο βγάζει αυτή η ανάλυση).
Τα αποτελέσματα αυτά είναι μάλλον άσχημα νέα και για την κοινότητα που προσπαθεί να ανιχνεύσει πειραματικά, σωματίδια σκοτεινής ύλης σε επίγειους ανιχνευτές τύπου DAMA. Όπως και να έχει όμως, δημιουργούνται πολλά ενδιαφέροντα ερωτήματα από όλα τα παραπάνω και αυτό επισημαίνουν και στην εργασία τους οι Bidin et al.
Έχει ενδιαφέρον πάντως το γεγονός ότι το αποτέλεσμα αυτό έρχεται λίγο μετά από ένα άλλο αποτέλεσμα σχετικά με την έμμεση ανίχνευση σκοτεινής ύλης, το οποίο είναι αυτό,
A Tentative Gamma-Ray Line from Dark Matter Annihilation at the Fermi Large Area Telescope, και για το οποίο μπορεί να διαβάσει κανείς λεπτομέρειες στο σχετικό άρθρο του Résonaances, Dark matter signal in Fermi?
Η όλη ιδέα με το τελευταίο είναι ότι η ασθενώς αλληλεπιδρούσα σκοτεινή ύλη θα μπορούσε να παράγει πολύ χαρακτηριστικές γραμμές φωτονίων γάμμα, τις οποίες φαίνεται να υποψιάζεται ότι ανίχνευσε το FERMI από την περιοχή του Γαλαξιακού κέντρου. Φυσικά και αυτό το θέμα έχει ψωμί ακόμα.
Δυστυχώς, επειδή το συγκεκριμένο θέμα είναι εκτός της ειδικότητάς μου, δεν μπόρεσα να το εξαντλήσω περισσότερο, αλλά θα δω μήπως και μπορέσουμε να έχουμε και την γνώμη κάποιου πιο ειδικού.
Αυτά προς το παρόν.
-----------------------------------------------
Update: Πολύ ενδιαφέροντα σχόλια από τον Sean Carroll στο, Puzzles!, στο blog Cosmic Variance, σχετικά με το θέμα της σκοτεινής ύλης και διάφορα τελευταία αποτελέσματα μετρήσεων.